2025年高职单招《数学》每日一练试题06月04日
2025-06-04 14:53:13 来源:人人学历网
2025年高职单招《数学》每日一练试题06月04日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
判断题
1、已知函数f(x)的定义域为[-1,5]、在同一坐标系下,函数y=f(x)的图象与直线x=1的交点个数为( )
答 案:对
解 析:∵f(x)的定义域为[-1,5],而1∈[-1,5],∴点(1,f(1))在函数y=f(x)的图象上。而点(1,f(1))又在直线x=1上,∴直线x=1与函数y=f(x)的图象至少有一个交点(1,f(1))。根据函数的定义知,函数是一个特殊的映射,即对于定义域[-1,5]中的任何一个元素,在其值域中只有唯一确定的元素f(1)与之对应,故直线x=1与y=f(x)的图象有且只有一个交点。
2、已知集合A={-1,0,1,2},B={x|x<0},则A∩B={-1,0}.
答 案:错
解 析:A∩B是集合A和集合B中相同元素的集合,即A∩B={-1).
单选题
1、下面4种说法: (1)一个有理数与一个无理数的和一定是无理数; (2)一个有理数与一个无理数的积一定是无理数; (3)两个无理数的和一定是无理数; (4)两个无理数的积一定是无理数。其中,正确的说法个数为()
- A:1
- B:2
- C:3
- D:4
答 案:A
解 析:(1)因为无理数是无限不循环小数,所以一个有理数与其相加必为无理数,故本小题正确;(2)0是有理数,故本小题错误;(3)正负相加则为0,故本小题错误;(4)二个无理数的积一定是无理数"是错误的,如√2*√2=2是有理数,故本小题错误
2、如果α是锐角,且sinα=3/5,那么cos(90°-α)的值为()
- A:4/5
- B:3/5
- C:3/4
- D:4/3
答 案:B
解 析:α是锐角,且sinα=3/5,cos(90°﹣α)=sina=3/5。故选B
多选题
1、已知等差数列{an}的前n项和为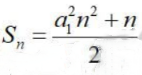 ,公差为d,则()
,公差为d,则()
- A:a1=1
- B:d=1
- C:
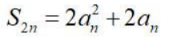
- D:2Sn-an=1+3+5+...+(2n-1)
答 案:ABD
2、下列计算结果正确的是()
- A:

- B:
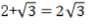
- C:
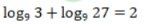
- D:
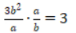
答 案:AC
主观题
1、已知抛物线C:x2=4y和直线7:2x+2y+m=0. (1)若抛物线C和直线l有两个交点,求m的取值范围; (2)若m>1,且直线l与抛物线C有两个交点A,B,线段AB的垂直平分线交y轴于点P,求△PAB的面积S的取值范围。
答 案:(1)由2x+2y+m=0得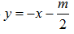 将其代入x2=4y中得x2+4x+2m=0,
所以△=42-4×1×2m=16-8m.
因为抛物线C和直线l有两个交点,所以△=16-8m>0,解得m<2.
因此,m的取值范围是(-∞,2)
(2)设点A(x1,,y1),B(x2,y2),则由方程x2+4x+2m=0可得x1+x2=-4,x1x2=2m,
(x1-x2)2=(x1+x2)2-4x1x2=8(2-m);
将其代入x2=4y中得x2+4x+2m=0,
所以△=42-4×1×2m=16-8m.
因为抛物线C和直线l有两个交点,所以△=16-8m>0,解得m<2.
因此,m的取值范围是(-∞,2)
(2)设点A(x1,,y1),B(x2,y2),则由方程x2+4x+2m=0可得x1+x2=-4,x1x2=2m,
(x1-x2)2=(x1+x2)2-4x1x2=8(2-m);
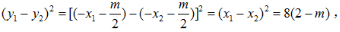 所以
所以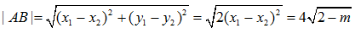 因为
因为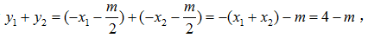 所以线段AB的中点
所以线段AB的中点 kAB=-1,
所以过点Q与线段AB垂直的直线方程为
kAB=-1,
所以过点Q与线段AB垂直的直线方程为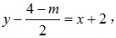 即2x-2y+8-m=0.
该直线与y轴的交点
即2x-2y+8-m=0.
该直线与y轴的交点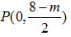 到直线l的距离
到直线l的距离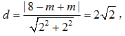 所以△PAB的面积
所以△PAB的面积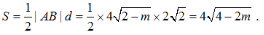 因为1<m<2,所以0<4-2m<2,
因为1<m<2,所以0<4-2m<2,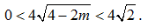 因此,△PAB的面积S的取值范围是(0,4√2)
因此,△PAB的面积S的取值范围是(0,4√2)
2、设函数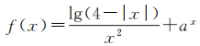 ,a>0且a≠1.
(1)求函数f(x)的定义域;
(2)若f(-3)=8,求实数a的值,并判断函数f(x)的奇偶性.
,a>0且a≠1.
(1)求函数f(x)的定义域;
(2)若f(-3)=8,求实数a的值,并判断函数f(x)的奇偶性.
答 案:(1)由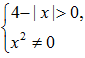 ,得
,得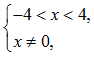 即有-4<x<0或0<x<4
因此,函数f(x)的定义域为{x|-4<x<0或0<x<4}
(2)因为
即有-4<x<0或0<x<4
因此,函数f(x)的定义域为{x|-4<x<0或0<x<4}
(2)因为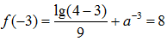 所以
所以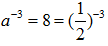 ,解得
,解得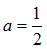 因为
因为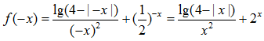 所以f(-x)≠-f(x),且f(-x)≠f(x).
因此,函数f(x)既不是奇函数也不是偶函数
所以f(-x)≠-f(x),且f(-x)≠f(x).
因此,函数f(x)既不是奇函数也不是偶函数
填空题
1、满足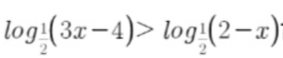 的x的集合是_____.
的x的集合是_____.
答 案: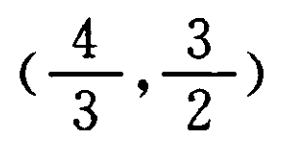
解 析:
2、“x∈A∩B”是“x∈AUB”的()条件。
答 案:充分不必要
解 析:可通过画集合的Venn图得到“x∈A∩B”是“x∈AUB”的充分不必要条件.



