2024年成考高起点《数学(理)》每日一练试题02月22日
2024-02-22 12:11:16 来源:人人学历网
2024年成考高起点《数学(理)》每日一练试题02月22日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、在△ABC中,若b=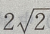 ,c=
,c=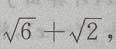
 则a等于()
则a等于()
- A:2
- B:
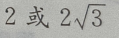
- C:
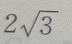
- D:无解
答 案:B
解 析:此题是已知两边和其中一边的对角,解三角形时,会出现一解、两解、无解的情况,要注意这一点.用余弦定理 可得
可得

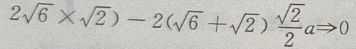
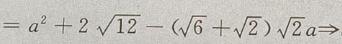
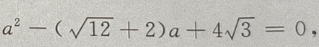 解出
解出


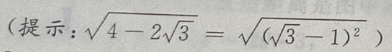
2、已知偶函数y=f(x),在区间[a,b](0 答 案:B 解 析:由偶函数的性质:偶函数在[a,b]和[-b,-a]上有相反的单调性,可知,y=f(x)在区间[a,b](0 3、过点P(2,3)且在两轴上截距相等的直线方程为()
答 案:B 解 析:选项A中, 4、在 答 案:D 解 析:直接套用二项式展开公式: 主观题 1、设函数f(x)=xlnx+x.(I)求曲线y=f(x)在点((1,f(1))处的切线方程; 答 案:(I)f(1)=1,f'(x)=2+lnx,故f'(1)=2.所以曲线y=f(x)在点(1,f(1))处的切线方程为y=2x-1.(II)令f'(x)=0,解得 2、为了测河的宽,在岸边选定两点A和B,望对岸标记物C,测得 答 案:如图, 3、已知直线l的斜率为1,l过抛物线C: 答 案:(I)C的焦点为 4、在△ABC中,B=120°,BC=4,△ABC的面积为 答 案:由△ABC的面积为 填空题 1、函数 答 案:2 解 析:当x=0时,y= 2、lg(tan43°tan45°tan47°)=()
答 案:0 解 析:lg(tan43°tan45°tan47°)=lg(tan43°tan45°cot43°)=lgtan45°=lg1=0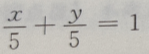
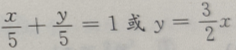
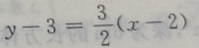
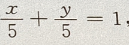 在x、y 轴上截距为 5.但答案不完整 所以选项B中有两个方程,
在x、y 轴上截距为 5.但答案不完整 所以选项B中有两个方程,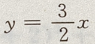 在x轴上横截距与y轴上的纵截距都为0,也是相等的
选项C,虽然过点(2,3),实质上与选项A相同.选项 D,转化为:
在x轴上横截距与y轴上的纵截距都为0,也是相等的
选项C,虽然过点(2,3),实质上与选项A相同.选项 D,转化为: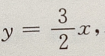 答案不完整
答案不完整
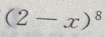 的展开式中,
的展开式中, 的系数是
的系数是 注:展开式中第r+1项的二项式系数
注:展开式中第r+1项的二项式系数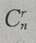 与第r+1项的系数不同,此题不能只写出
与第r+1项的系数不同,此题不能只写出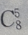 就为
就为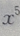 的系数
的系数
(II)求f(x)的极值. 当
当 时,f'(x)
时,f'(x) 单调递减,在区间
单调递减,在区间 单调递增.因此f(x)在
单调递增.因此f(x)在 时取得极小值
时取得极小值
 AB=120m,求河的宽
AB=120m,求河的宽

 ∵∠C=180°-30°-75°=75°
∴△ABC为等腰三角形,则AC=AB=120m
过C做CD⊥AB,则由Rt△ACD可求得CD=
∵∠C=180°-30°-75°=75°
∴△ABC为等腰三角形,则AC=AB=120m
过C做CD⊥AB,则由Rt△ACD可求得CD= =60m,
即河宽为60m
=60m,
即河宽为60m
 的焦点,且与C交于A,B两点.(I)求l与C的准线的交点坐标;
的焦点,且与C交于A,B两点.(I)求l与C的准线的交点坐标;
(II)求|AB|. ,准线为
,准线为 由题意得l的方程为
由题意得l的方程为 因此l与C的准线的交点坐标为
因此l与C的准线的交点坐标为 (II)由
(II)由 ,得
,得 设A(x1,y1),B(x2,y2),则
设A(x1,y1),B(x2,y2),则 因此
因此
 ,求AC.
,求AC. 得
得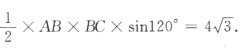 所以AB =4.因此
所以AB =4.因此 所以
所以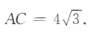
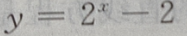 的图像与坐标轴的交点共有()
的图像与坐标轴的交点共有()
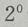 -2=-1,故函数与y轴交于(0,-1)点,令y=0,则有
-2=-1,故函数与y轴交于(0,-1)点,令y=0,则有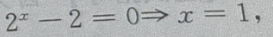 故函数与x轴交于(1,0) 点,因此函数
故函数与x轴交于(1,0) 点,因此函数 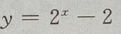 与坐标轴的交点共有 2个.
与坐标轴的交点共有 2个.



