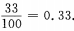2024年成考高起点《数学(理)》每日一练试题10月10日

2024年成考高起点《数学(理)》每日一练试题10月10日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、设函数f(x－2)＝x²－3x－2，则f(x)＝（）。

• A：x²＋x－4
• B：x²－x－4
• C：x²＋x＋4
• D：x²－x%－4

答 案：A

解 析：令x-2=t,得x=t+2代入原式,得f(t)=(t+2)²-3(t+2)-2=t²+t-4.即f(x)=x²+x-4.(答案为 A)

2、=（）。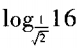

• A：8
• B：-8
• C：2
• D：-2

答 案：B

解 析：由于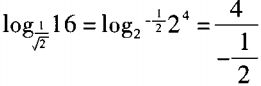。log2²=-8。故选B。

3、在定义域内下列函数中为增函数的是（）。

• A：f(x)＝2－x
• B：f(x)＝－log2x
• C：f(x)＝x³ 
• D：f(x)＝x²＋1

答 案：C

解 析：由函数的性质可知，f(x)＝x³为增函数。(答案为C)  

4、设二次函数f(x)=x²+px+q的图象经过点(1,一4)且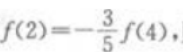则该二次函数的最小值为（）。

• A：－6
• B：－4
• C：0
• D：10

答 案：B

解 析：

主观题

1、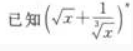 展开式的二项式系数之和比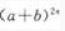展开式的二项式系数之和小240。 求：（1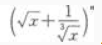）展开式的第3项；
（2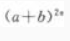）展开式的中间项。

答 案：

2、设a为实数，且tanα和tanβ是方程ax²+（2a-3）x+（a-2）=0的两个实根，求tan（α+β）的最小值。

答 案：由已知得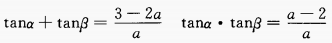

3、求函数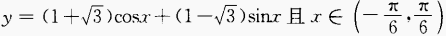上的最大值以及取得这个最大值的x。

答 案：.1 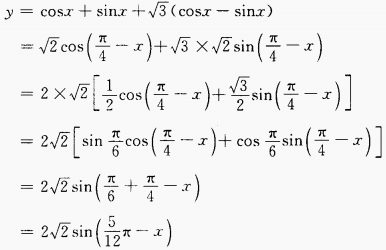函数取最大值，即y最大值=。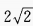

4、在正四棱柱ABCD-A'B'C'D'中， （Ⅰ）写出向量和关于基底{a,b,c}的分解式; （Ⅱ）求证： （Ⅲ）求证：  

答 案：（Ⅰ）由题意知(如图所示)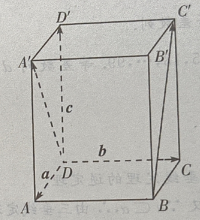  

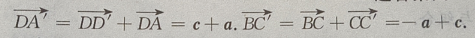
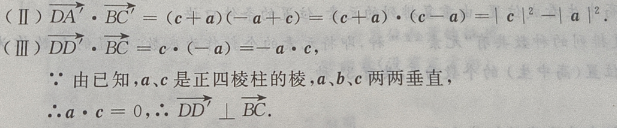
填空题

1、已知≤0＜2π，且实数x满足log₃x=2-cos²θ+sin²θ，则x的最小值是______。  

答 案：3

解 析：因为log₃x=2-（cos²θ-sin²θ）=2-cos2θ。 又log₃x中的底数3＞1，因此要使x最小，应使2-cos2θ的值最小，而其最小值为1，故x=3。

2、在自然数1、2、…、100中任取一个数，该数能被3整除的概率是______。  

答 案：0.33

解 析：此题随机试验包含的基本事件总数n=100，且每个数能被取到的机会均等，即属于等可能事件的概率能被3整除的自然数的个数m=33，故所求概率