2024年成考高起点《数学(理)》每日一练试题10月13日
2024-10-13 12:15:18 来源:人人学历网
2024年成考高起点《数学(理)》每日一练试题10月13日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、i为虚数单位,则复数 的虚部为()。
的虚部为()。
- A:
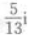
- B:
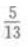
- C:

- D:
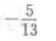
答 案:D
解 析:
2、“曲线C上的点的坐标都是方程f(x,y)=0的解”是“f(x,y)=0是曲线C的方程”的()。
- A:充分但非必要条件
- B:必要但非充分条件
- C:充要条件
- D:非充分非必要条件
答 案:B
3、已知2a=3,2b=6,2C=12,则().
- A:b2=a+c
- B:2b=ac
- C:2b=a+c
- D:b2=ac
答 案:C
解 析:由已知,2a·2c=36,即2a+c=36。又(2b)2=62,22b=36,则22b=2a+c,2b=a+c选C。
4、设log2x=a,则log2(2x2)=()。
- A:2a2+1
- B:2a2-1
- C:2a-1
- D:2a+1
答 案:D
解 析:本题主要考查的知识点为对数函数的性质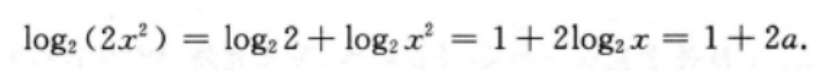
主观题
1、空间有四个点,如果其中任何三点不在同一直线上,可以确定几个平面?
答 案:根据公理,在所给定的四点中任取三点,可确定一个平面,由组合公式 所以共可确定四个平面。
所以共可确定四个平面。
解 析:空间有n个点,如果其中任何三点不在同一直线上,可以确定 个平面。
个平面。
2、求函数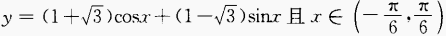 上的最大值以及取得这个最大值的x。
上的最大值以及取得这个最大值的x。
答 案:.1 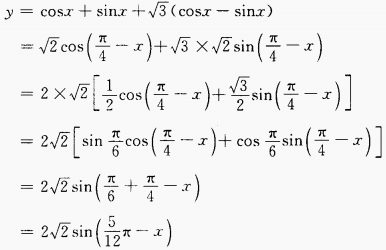
 函数取最大值,即y最大值=。
函数取最大值,即y最大值=。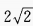
3、已知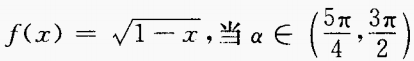 时,化简式子f(sin2α)-f(- sin2α)。
时,化简式子f(sin2α)-f(- sin2α)。
答 案:由已知得, 4、已知tan2θ=2tan2ψ+1,求cos2θ+sin2ψ的值。 答 案:由已知,得 填空题 1、已知 答 案: 解 析: 2、椭圆的中心在原点,一个顶点和一个焦点分别是直线x+3y-6与两坐标轴的交点,则此椭圆的标准方程为()
答 案: 解 析:原直线方程可化为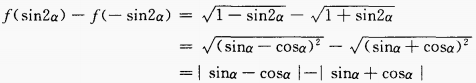
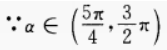 ∴sinα
∴sinα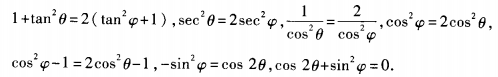
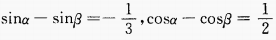 ,则
,则 =______。
=______。
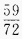
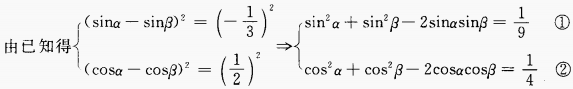
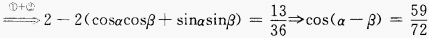
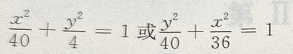
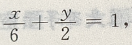 交点(6,0),(0,2). 当点(6,0)是椭圆一个焦点,点(0,2) 是椭圆一个顶点时,c=6,b=2,
交点(6,0),(0,2). 当点(6,0)是椭圆一个焦点,点(0,2) 是椭圆一个顶点时,c=6,b=2, 当点(0,2) 是椭圆一个焦点,(6,0) 是椭圆一个顶点时,c=2,b-6,
当点(0,2) 是椭圆一个焦点,(6,0) 是椭圆一个顶点时,c=2,b-6,



