2024年成考高起点《数学(文史)》每日一练试题12月25日

2024年成考高起点《数学(文史)》每日一练试题12月25日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、用列举法表示集合{（x，y）|x+2y=7且x，y为正整数}，结果是（）。  

• A：{x=5，3，1，y=1，2，3}
• B：{（5，1），（3，2）（1，3）}
• C：{（1，5），（2，3），（3，1）}
• D：{（7，0）（5，1）（3，2）（1，3）}

答 案：B

2、已知函数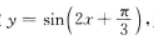，则下列命题中正确的是（　）

• A：它是奇函数
• B：它的图像是由y=sin2x向左平移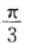得到的
• C：它的图象关于直线x=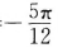成轴对称图形
• D：它的单调递增区间是

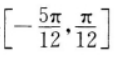
答 案：C

解 析：显然它不是奇函数，不能认为含有“sin”符号的函数就是奇函数，故A项错误．图象的平移要看函数式中的自变量z的变化情况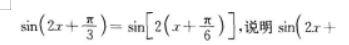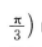． 的图象是把 sin2x 的图象向左平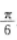。一般说来,sin(ωx+y)的图象是将sinωx 的图象沿x轴正方向平移了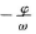而得到的,故B项错误,过函数y=sinx的每一个最大值点或最小值点(即使sinx=1或-1的点)作x轴的垂线,都是其函数图象的对称轴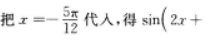 【考点指要】本题考查了三角函数的奇偶性、单调性以及图象的平移与对称轴，对三角函数的性质进行了较全面的考查．

3、△ABC中，已知AC=12，∠A=30°，∠B=120°，则BC=（）

• A：
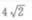
• B：
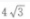
• C：
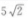
• D：

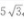
答 案：B

4、若向量a=（x，-2），b=（-2，1），且a//b，则x=（）。

• A：-4
• B：-1
• C：1
• D：4

答 案：D

主观题

1、已知函数f（x）=2x³-3x²，求
（1）函数的单调区间；

（2）函数f（x）在区间[-3，2]的最大值与最小值。

答 案：

2、设函数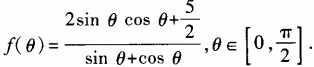 （1）求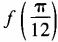；（2）求函数f（θ）最小值。

答 案：

3、设椭圆的中心是坐标原点,长轴在x轴上,离心率已知点P到圆上的点的最远距离是求椭圆的方程  

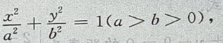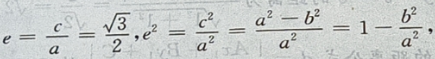
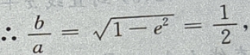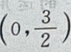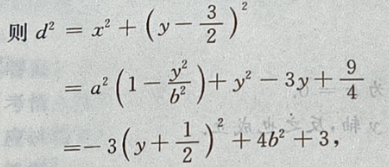
答 案：由题意，设椭圆方程为 由 设P点到椭圆上任一点的距离为 d, 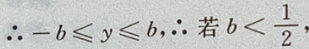则在y=-b时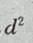，最大，即d也最大。  

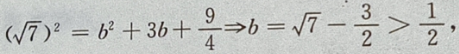
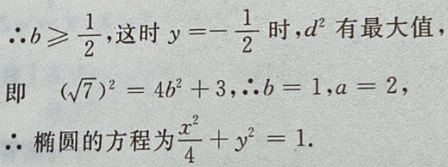
4、求下列函数的最大值、最小值和最小正周期： （1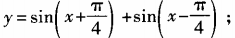） 2）y=6cosx+8sinx

答 案： 所以函数的最大值是最小值是最小正周期为2π， （2）要将6cosx+8sinx化为sinαcosx+cosαsinx这种形式，需使cosx与sinx的系数平方和为1，为此，将已知函数化为 因此,函数的最大值是10,最小值是-10,最小正周期为2π

填空题

1、已知tanθ=1/2，则sin2θ+sin2θ=__________．

答 案：1

解 析：

2、已知tanα=2，则=______。  

答 案：