2024年成考高起点《数学(文史)》每日一练试题12月28日

2024年成考高起点《数学(文史)》每日一练试题12月28日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、设α是第一象限角，则sin2α=（）。

• A：
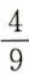
• B：
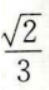
• C：
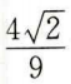
• D：

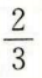
答 案：C

解 析：本题主要考查的知识点为三角函数的二倍角公式。 α在第一象限，则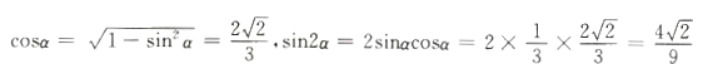

2、已知一个等差数列的第五项等于10，前三项的和等于3，那么这个等差数列的公差为（）。

• A：3
• B：1
• C：-1
• D：-3

答 案：A

3、设集合P=（1，2，3，4，5），Q={2，4，6，8，10}，则集合P∩Q=（）。  

• A：｛2，4}
• B：｛1，2，3，4，5，6，8，10}
• C：｛2｝
• D：｛4｝

答 案：A

4、已知3sin²α+8sinα-3=0，则cos2α=（）。

• A：
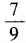
• B：
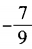
• C：
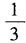
• D：

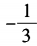
答 案：A

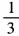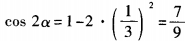解 析：由已知得（3sinα-1）（sinα+3）=0。 由于|sinα|≤1，所以sinα=。因此。故选A。

主观题

1、已知tan²θ=2tan²ψ+1，求cos2θ+sin²ψ的值。  

答 案：由已知，得

2、一艘渔船在航行中遇险，发出警报，在遇险地点西南10海里处有一艘货轮，接收到报时，发现遇险渔船正以9海里/小时的速度与沿南偏东75°方向向某小岛靠近，如果要在40分内将这艘渔船救出，求货轮航行的方向和速度。

答 案：货轮沿东偏北21.8°的方向，以21海里/小时的船速航行。

3、在△ABC中，B=120°,C=30°,BC=4，求△ABC的面积．

答 案：因为A= 180°-B-C=30°，所以AB = BC=4.因此△ABC的面积

4、已知a,b,c成等比数列，x是a，b的等差中项，y是b，c的等差中项证明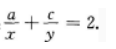  

答 案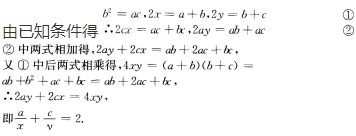： 考点 本题考查考生对等差中项和等比中项公式的理解及运用．

填空题

1、不等式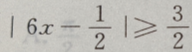的解集是（）  

答 案：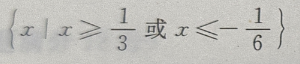

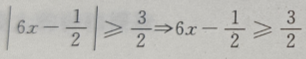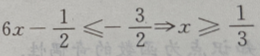解 析：或或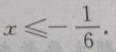

2、5个同学站成一排，其中某个人恰好站在排头的概率是______。  

答 案：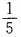

解 析：基本事件的总数n=5！，其中某人恰好站在排头的排法有m=4！种，所求概率为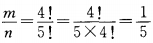。