2024年成考高起点《数学(文史)》每日一练试题12月29日

2024年成考高起点《数学(文史)》每日一练试题12月29日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、下列函数图象与y=f（x）的图象关于原点对称的是（）。  

• A：y=-f（x）
• B：y=f（-x）
• C：y=-f（-x）
• D：y=｜f（x）｜

答 案：C

2、已知集合A={0，1，2，3，4}，B={x|0＜x＜4}，则A∩B=（）。  

• A：{0，1，2，3}
• B：{1，2，3}
• C：{1，2}
• D：{0，4}

答 案：B

3、设M=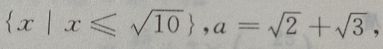那么（）

• A：
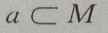
• B：
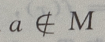
• C：
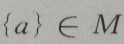
• D：

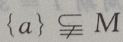
答 案：D

解 析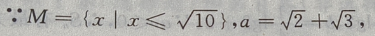： M是集合，a为元素，{a}为集合，元素与集合的关系是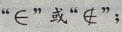集合与集合的关系是  

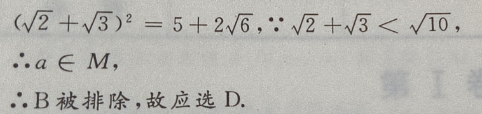
4、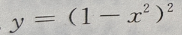的导数是  

• A：
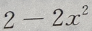
• B：
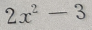
• C：
• D：

答 案：C

解 析：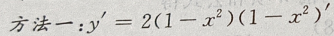

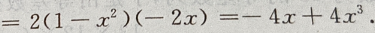
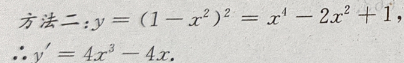
主观题

1、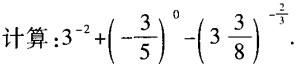  

答 案：

2、cos20°cos40°cos80°的值。  

答 案：

3、设函数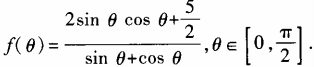 （1）求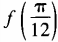；（2）求函数f（θ）最小值。

答 案：

4、已知函数ƒ(x)=ax3-x2+bx+1(a，b∈R)在区间(-∞，0)和(1，+∞)上都是增函数，在(0，1)内是减函数． (Ⅰ)求a，b的值； (Ⅱ)求曲线y=ƒ(x)在x=3处的切线方程．

答 案：(Ⅰ)因为函数ƒ(x)在(-∞，0)上递增，在（0,1）内递减，在（1，+∞）上有递增，可知函数在x=0和x=1处的导数值均为0. 又f’(x)=3ax²-2x+b, 所以f’(0)=b=0,f’(1)=3a-2+b=0. 即切点为(3.10),所以其切线方程为y-10=12(x-3),即12x-y-26 = 0.  

解 析：【考点指要】本题主要考查函数导数的几何意义、导数的求法和导数的应用——函数的单调区间及曲线的切线方程的求法  

填空题

1、已知tanθ=1/2，则sin2θ+sin2θ=__________．

答 案：1

解 析：

2、从某班的一次数学测试卷中任意抽出10份,其得分情况如下:81,98,43,75,60,55,78,84,90,70,则这次测验成绩的样本方差是（）  

答 案：252.84

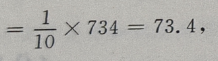
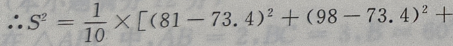
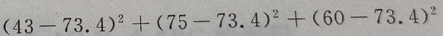
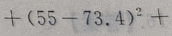
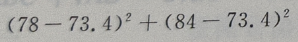
解 析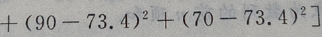： =252.84