2024年成考高起点《数学(文史)》每日一练试题12月30日

2024年成考高起点《数学(文史)》每日一练试题12月30日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、从13名学生中选出2人担任正副班长，不同的选举结果共有（）。

• A：26
• B：78
• C：156
• D：169

答 案：C

2、若log₁₅5=m，则log₁₅3=（）。

• A：
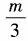
• B：1+m
• C：1-m
• D：m-1

答 案：C

解 析：log₁₅3=log₁₅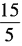=log₁₅15-log₁₅5=1-m选C。

3、点(2,4)关于直线y=x的对称点的坐标为（）  

• A：(4,2)
• B：(-2,-4)
• C：(-2,4)
• D：(-4,-2)

答 案：A

解 析：点(2,4) 关于直线y=x对称的点为(4,2)

4、点P(-5,12)到y轴的距离（）  

• A：12
• B：7
• C：-5
• D：5

答 案：D

解 析：由点P的坐标（-5,12）知，点P到y轴的距离为|x|=5

主观题

1、已知三角形的一个内角是，面积是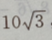周长是20,求各边的长.  

答 案：设三角形三边分别为a,b,c,∠A=60°，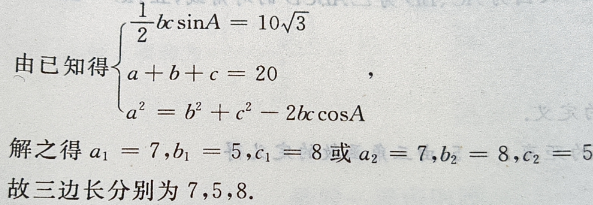  

2、设全集U=R，集合A={x｜-5＜x＜5}，B={x｜0≤x≤7}，求CUA∩B．

答 案：解：全集U=R，A={x｜-5＜x＜5}，B=｛X｜0≤x≤7}，因为CuA={x｜x≤-5或x≥5}，所以CuA∩B={x｜x≤-5或x≥5}N{x｜0≤x≤7}={x｜5≤x≤7}，如图1—10所示。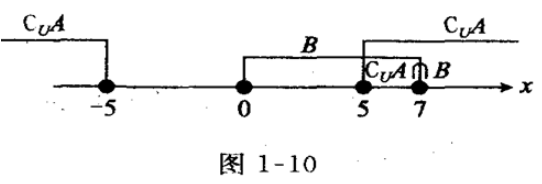

3、如图：已知在△ADC中，∠C=90°，∠D=30°，∠ABC=45°，BD=20，求AC(用小数表示，保留一位小数)  

答 案：如图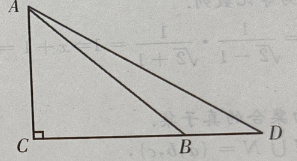  

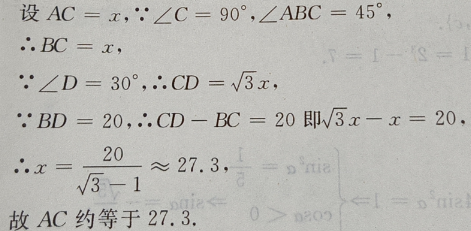
4、求下列函数的最大值、最小值和最小正周期： （1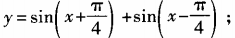） 2）y=6cosx+8sinx

答 案： 所以函数的最大值是最小值是最小正周期为2π， （2）要将6cosx+8sinx化为sinαcosx+cosαsinx这种形式，需使cosx与sinx的系数平方和为1，为此，将已知函数化为 因此,函数的最大值是10,最小值是-10,最小正周期为2π

填空题

1、在∆ABC中，已知cosA=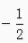，cosB=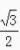，那么cosC=______。

答 案：

2、函数f(x)=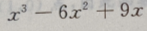在区间[-3,3]上的最大值为（）  

答 案：4

解 析：这题考的是高次函数的最值问题，可用导数来求函数在区间[-3,3]上的最值。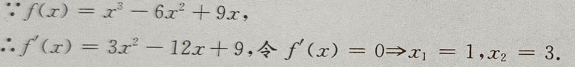 列出表格 由上表可知函数在[-3,3]上，在x=1点处有最大值为4.