2024年成考高起点《数学(文史)》每日一练试题12月31日

2024年成考高起点《数学(文史)》每日一练试题12月31日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、（）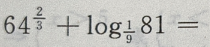  

• A：8
• B：14
• C：12
• D：10

答 案：B

解 析：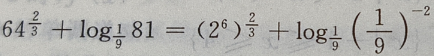

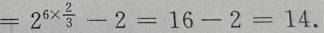
2、如果点A（1，1）和B（2，4）关于直线y=kx+b对称，则k=（）。  

• A：-3
• B：
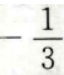
• C：
• D：3

答 案：B

解 析：本题主要考查的知识点为两垂直直线斜率的关系。 直线AB的斜率为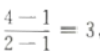：点A、B关于直线y=kx+b对称，因此直线AB与其垂直，故3k=-1，得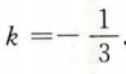

3、若-1，a,b,c,-9五个数列成等比数列，则（）

• A：b=3,ac=9
• B：b=-3,ac=9
• C：b=-3,ac=-9
• D：b=3,ac=-9

答 案：B

解 析：因为-1，a,b,c,-9成等比数列，所以ac=b2=-1×(-9)=9,所以ac=9，b=±3，又因为-1，a,b成等比数列，所以a2=-b＞0，所以b=-3  

4、用1,2,3,4一组成没有重复数字的三位数，其中偶数共有（）

• A：24个
• B：12个
• C：6个
• D：3个

答 案：B

解 析：若三位数为偶数，个位数只能从2,4中选一个，故没有重复数字的偶数三位数为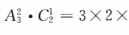

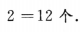
主观题

1、已知a^m=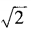，aⁿ=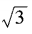，求a^3n-4m的值。  

答 案：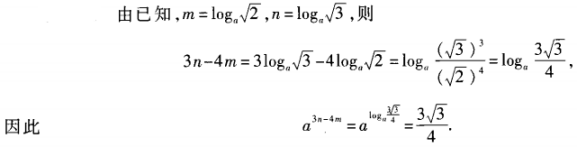

2、设椭圆的中心是坐标原点,长轴在x轴上,离心率已知点P到圆上的点的最远距离是求椭圆的方程  

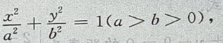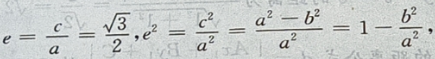
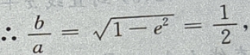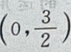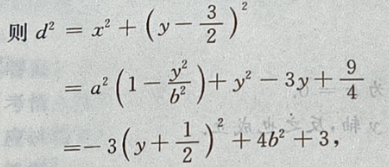
答 案：由题意，设椭圆方程为 由 设P点到椭圆上任一点的距离为 d, 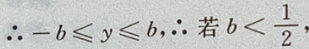则在y=-b时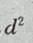，最大，即d也最大。  

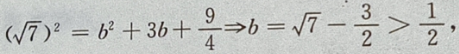
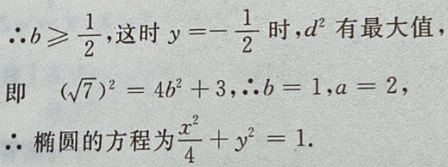
3、设全集U=R，集合A={x｜-5＜x＜5}，B={x｜0≤x≤7}，求CUA∩B．

答 案：解：全集U=R，A={x｜-5＜x＜5}，B=｛X｜0≤x≤7}，因为CuA={x｜x≤-5或x≥5}，所以CuA∩B={x｜x≤-5或x≥5}N{x｜0≤x≤7}={x｜5≤x≤7}，如图1—10所示。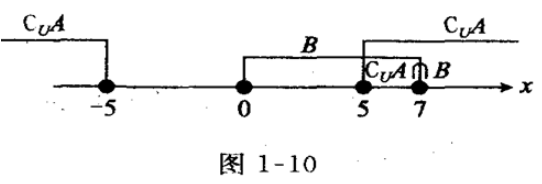

4、已知tan²θ=2tan²ψ+1，求cos2θ+sin²ψ的值。  

答 案：由已知，得

填空题

1、袋中装有3个白球，2个红球，从中任取2个球，取到2个都是红球的概率是______。  

答 案：

解 析：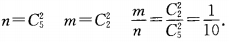

2、平面内有10个点，任何三点都不在同一直线上，问能连成______条不同的直线。  

答 案：45