2025年成考高起点《数学(理)》每日一练试题01月02日

2025年成考高起点《数学(理)》每日一练试题01月02日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、5名高中毕业生报考3所院校,每人只能报一所院校,则有（）种不同的报名方法  

• A：
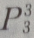
• B：
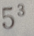
• C：
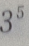
• D：

答 案：C

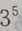解 析：将院校看成元素,高中生看成位置,由重复排列的元素、位置的条件口诀: “元素可挑剩，位置不可缺”，重复排列的种数共有种,即将元素的个数作为底数,位置的个数作为指数.即:元素(院校)的个数为 3,位置(高中生)的个数为5,共有种。  

2、以椭圆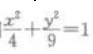上任一点(长轴两端除外)和两个焦点为顶点的三角形的周长等于（）。

• A：
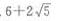
• B：
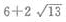
• C：
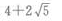
• D：

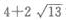
答 案：A

解 析：由椭圆方程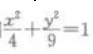 可知a²=9,b²=4,则 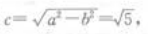则椭圆上任一点(长轴两端除外)和两个焦点为顶点的三角形的周长等于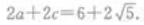

3、分别和两条异面直线AB、CD同时相交的两条直线AC、BD（）。

• A：相交
• B：平行
• C：是异面直线
• D：垂直

答 案：C

4、函数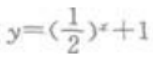的值域是（）。

• A：(0，＋∞)
• B：(－∞，＋∞)
• C：(1，＋∞)
• D：[1，＋∞)

答 案：C

解 析：

主观题

1、已知lg2=a，lg3=b，求lg0.15关于a，b的表达式。  

答 案：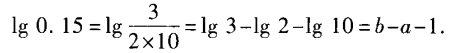

2、设（0＜α＜π），求tanα的值。

答 案：

3、（1）已知tanα=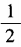，求cot2α的值； （2）已知tan2α=1，求tanα的值。

答 案：（1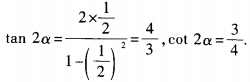）（2）由已知，得 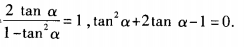解关于tanα的一元二次方程，得tanα=  

4、为了测河的宽,在岸边选定两点A和B,望对岸标记物C,测得AB=120m,求河的宽

答 案：如图， ∵∠C=180°-30°-75°=75° ∴△ABC为等腰三角形，则AC=AB=120m 过C做CD⊥AB,则由Rt△ACD可求得CD==60m， 即河宽为60m  

填空题

1、在△ABC中，已知a=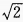+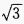，则bcosC+ccosB=______。  

答 案：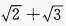

解 析：由余弦定理得，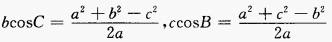  

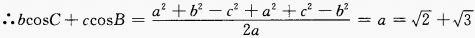
2、长方体的长、宽、高分别为2,3,6，则该长方体的对角线长为（）

答 案：7

解 析：由题可知长方体的底面的对角线长为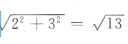，则在由高、底面对角线、长方体的对角线组成的三角形中，长方体的对角线长为