2025年成考高起点《数学(理)》每日一练试题01月04日
2025-01-04 12:07:13 来源:人人学历网
2025年成考高起点《数学(理)》每日一练试题01月04日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、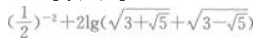 ()。
()。
- A:3
- B:4
- C:5
- D:6
答 案:C
解 析: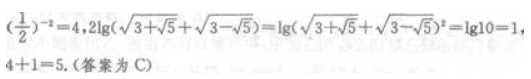
2、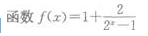 ()。
()。
- A:是奇函数
- B:是偶函数
- C:既是奇函数,又是偶函数
- D:既不是奇函数,又不是偶函数
答 案:A
解 析:
3、中心在坐标原点,一个焦点的坐标是(-3,0),一条渐近线方程式 的双曲线方程是()。
的双曲线方程是()。
- A:
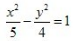
- B:
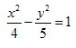
- C:
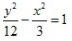
- D:
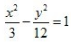
答 案:B
4、sinθ·cosθ·tanθ<0,则θ属于集合()。
- A:{θ|<0<π}
- B:{θ|<0<
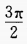 }
} - C:Ø
- D:{θ|-
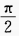 <θ<0}
<θ<0}
答 案:C
解 析:sinθ·cosθ·tanθ=sin2θ<0,这样的角不存在。
主观题
1、在△ABC中如果sinA=2sinBcosC,求证:△ABC是等腰三角形。
答 案: ∴△ABC为等腰三角形。
∴△ABC为等腰三角形。
2、求下列函数的最大值、最小值和最小正周期: (1)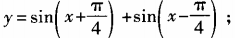 (2)y=6cosx+8sinx
(2)y=6cosx+8sinx
答 案:
3、已知A(1,4),B(3,8),C(4,10)。求证A、B、C三点共线。
答 案: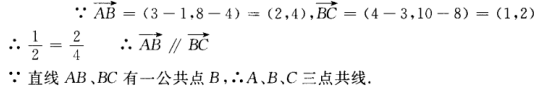
4、已知抛物线C:y2=2px(p>0)的焦点到准线的距离为1。 (I)求C的方程; (Ⅱ)若A(1,m)(m>0)为C上一点,O为坐标原点,求C上另一点B的坐标,使得OA⊥OB
答 案:(I)由题意,该抛物线的焦点到准线的距离为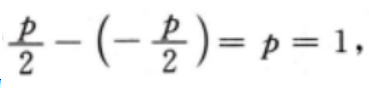 所以抛物线C的方程为
所以抛物线C的方程为 (Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得
(Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得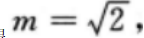 因此A点坐标为
因此A点坐标为 设B点坐标为
设B点坐标为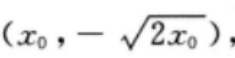 则
则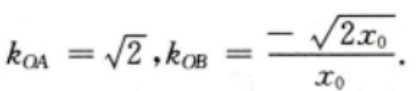 因为
因为 则有
则有 即
即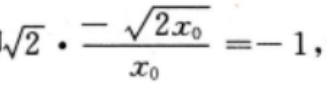 解得x0=4
所以B点的坐标为
解得x0=4
所以B点的坐标为
填空题
1、曲线y=在点(1,1)处的切线方程是______。
答 案:2x+y-3=0
解 析:本题主要考查的知识点为切线方程
由题意,该切线斜率,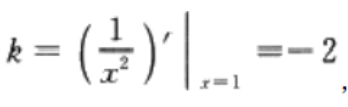 又过点(1,1),所以切线方程为y-1=-2(x-1)
又过点(1,1),所以切线方程为y-1=-2(x-1)
2、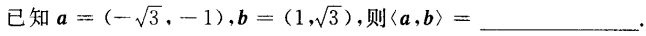
答 案:;150°
解 析: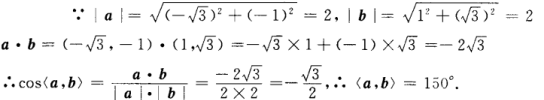
温馨提示:因考试政策、内容不断变化与调整,本站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!
热门资讯
猜你喜欢
换一换
成人高考加分条件有哪些 成考怎么进行加分
01-26
山东省2025年上半年高等学历继续教育学士学位外语考试报名时间
01-03
黑龙江省2025年高职院校单独招生考试有关工作安排的通知
12-28
河南财经政法大学2025年成人本科学士学位申请时间安排
01-03
黑龙江2025年高职单招考试时间及科目安排
12-26
2025年海南省高职分类招生考试报名时间安排
12-20
江西高职单招2025公告
12-11
江西高职单招考试时间2025
12-11



