2025年成考高起点《数学(文史)》每日一练试题01月04日

2025年成考高起点《数学(文史)》每日一练试题01月04日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、直线l₁与直线l₂：3x+2y-12=0的交点在x轴上，并且l₁⊥l₂，则l₁在y轴上的截距是（）。

• A：-4
• B：
• C：4
• D：

答 案：B

解 析：由于直线l2:3x+2y-12=0与x轴的交点为（4,0），斜率为故直线l1的斜率为，且经过（4,0），故l1的方程为y-0=令x=0求得，即l1在y轴上的截距是故选C。 用点斜式求得直线l1的方程，再根据直线在y轴上的截距的定义求得l1在y轴上的截距，本题主要考查用点斜式求直线的方程，直线在y轴上的截距的定义和求法，属于基础题

2、

• A：(-∞，-6)∪(1，+∞)
• B：(-6，1)
• C：(-∞，2)∪(3，+∞)
• D：(2，3)

答 案：B

解 析： 求必须有6-5x-x2>0，即x2+5x-6<0，即(x+6)(x-1)<0，解得-6，用区间表示为(-6，1)．此处应注意分母不能为零． 【考点指要】本题要求按二次根式定义域来解一元二次不等式，求定义域是成人高考的常见题．

3、函数y=-x²+2x的值域是（）。  

• A：[0,+∞)
• B：[1,+∞)
• C：(-∞,1]
• D：(-∞,0)

答 案：C

解 析：本题主要考查的知识点为函数的值域. y=-x²+2x=1-(x-1)²≤1，故原函数的值域为(-∞,1]

4、下列函数中，为减函数的是（）

• A：y=cosx
• B：
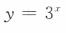
• C：
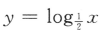
• D：

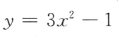
答 案：C

解 析：由对数函数的性质可知，当底数大于0小于1时，在定义域内，对数函数为减函数，故选C选项．

主观题

1、（1）已知tanα=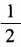 求cot2α的值； （2）已知tan2α=1，求tanα的值。

答 案：（1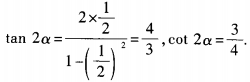） （2）由已知，得 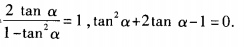解关于tanα的一元二次方程，得tanα=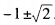

2、已知x+x^-1=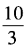，求x²+x^-2的值。  

答 案：由已知，得

3、已知抛物线C：y2=2px（p>0）的焦点到准线的距离为1。（I）求C的方程；
（Ⅱ）若A（1，m）（m>0）为C上一点，O为坐标原点，求C上另一点B的坐标，使得OA⊥OB。

答 案：(I)由题意,该抛物线的焦点到准线的距离为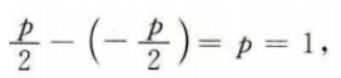 所以抛物线C的方程为y²=2x. (Ⅱ)因A(l,m)(m>0)为C上一点,故有m²=2, 可得 m=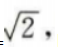因此A点坐标为 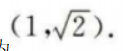设B点坐标为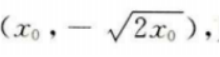

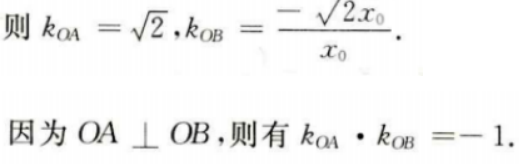
4、已知三角形的一个内角是，面积是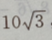周长是20,求各边的长.  

答 案：设三角形三边分别为a,b,c,∠A=60°，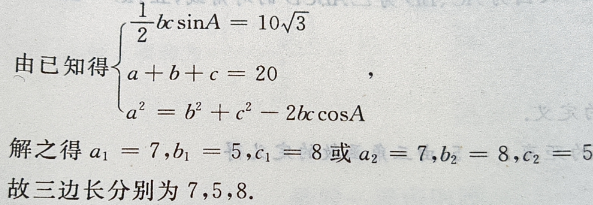  

填空题

1、与已知直线7x+24y-5=0平行，且距离等于3的直线方程是______。  

答 案：7x+24y+70=0或7x+24y-80=0

解 析：设要求的直线方程为7x+24y+c=0， ∵直线7x+24y+c=0到直线7x+24y-5=0的距离等于3 ∴ ∴.C=70或-80. 故所求的直线方程为7x+24y+70=0或7x+24y-80=0

2、直线的倾斜角的度数为（）  

答 案：60°

解 析：由题意知直线的斜率为设直线的倾斜角为α，则tanα=由0°≤α≤180°，故α=60°