2025年成考高起点《数学(文史)》每日一练试题01月05日

2025年成考高起点《数学(文史)》每日一练试题01月05日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、对任意两个集合A，B，下列命题中正确的是（　）

• A：
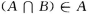
• B：
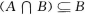
• C：
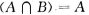
• D：

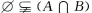
答 案：B

解 析：

2、设α=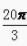，则（）。  

• A：sinα＞0，cosα＜0
• B：sinα＞0，cosα＞0
• C：sinα＜0，cosα＞0
• D：sinα＜0，cosα＜0

答 案：A

3、设集合P=（1，2，3，4，5），Q={2，4，6，8，10}，则集合P∩Q=（）。  

• A：｛2，4}
• B：｛1，2，3，4，5，6，8，10}
• C：｛2｝
• D：｛4｝

答 案：A

4、已知3sin²α+8sinα-3=0，则cos2α=（）。

• A：
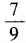
• B：
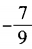
• C：
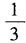
• D：

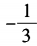
答 案：A

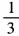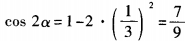解 析：由已知得（3sinα-1）（sinα+3）=0。 由于|sinα|≤1，所以sinα=。因此。故选A。

主观题

1、设函数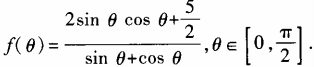 （1）求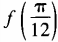；（2）求函数f（θ）最小值。

答 案：

2、已知三角形的一个内角是，面积是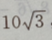周长是20,求各边的长.  

答 案：设三角形三边分别为a,b,c,∠A=60°，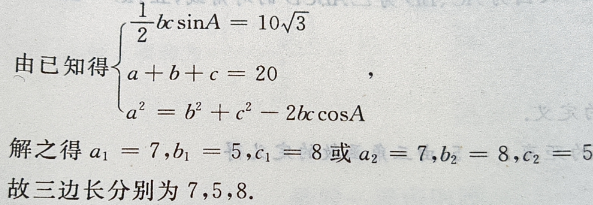  

3、已知函数ƒ(x)=ax3-x2+bx+1(a，b∈R)在区间(-∞，0)和(1，+∞)上都是增函数，在(0，1)内是减函数． (Ⅰ)求a，b的值； (Ⅱ)求曲线y=ƒ(x)在x=3处的切线方程．

答 案：(Ⅰ)因为函数ƒ(x)在(-∞，0)上递增，在（0,1）内递减，在（1，+∞）上有递增，可知函数在x=0和x=1处的导数值均为0. 又f’(x)=3ax²-2x+b, 所以f’(0)=b=0,f’(1)=3a-2+b=0. 即切点为(3.10),所以其切线方程为y-10=12(x-3),即12x-y-26 = 0.  

解 析：【考点指要】本题主要考查函数导数的几何意义、导数的求法和导数的应用——函数的单调区间及曲线的切线方程的求法  

4、已知直线l的斜率为1，l过抛物线C：的焦点，且与C交于A,B两点.
(I）求l与C的准线的交点坐标；
(II）求|AB|．

答 案：(I）C的焦点为，准线为由题意得l的方程为因此l与C的准线的交点坐标为(II）由得设A（x1,y1）.B（x2,y2），则因此

填空题

1、函数y=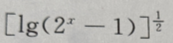的定义域是（）

答 案：[1,+∞)

解 析：要是函数y=有意义，需使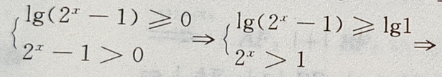 所以函数的定义域为{x|x≥1}=[1,+∞)  

2、过点（2，0）作圆x2+y2=1的切线，切点的横坐标为（）。

答 案：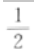

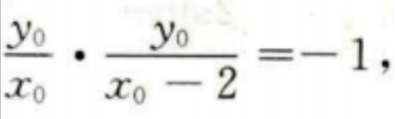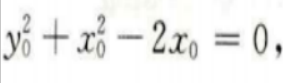
解 析：本题主要考查的知识点为圆的切线. 设切点(x0,y0)则有 即所以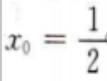故切点横坐标为