2025年成考高起点《数学(文史)》每日一练试题01月13日

2025年成考高起点《数学(文史)》每日一练试题01月13日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、已知tanα+sinα=m，tanα-sinα=n（m+n≠0），则cosα的值是（）。  

• A：
• B：
• C：
• D：

答 案：A

2、函数y=2x³+3x²-12x+1在区间(-2，1)内是（　）

• A：单调递增
• B：单调递减
• C：不增不减
• D：有增有减

答 案：B

解 析：y´=6x²+6x-12，在区间(-2，1)内y´<0，所以函数在区间(-2，1)内是单调递减的． 【考点指要】本题主要考查利用导数讨论函数的单调性问题，考试大纲要求会用这种方法讨论函数的性质．

3、设集合A={x|x2-2x-32}，则A∩B=（　）

• A：{x|-1
• B：{x|03}
• C：{x|-3
• D：{x|0

答 案：A

4、函数与y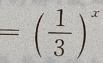的图像之间的关系是  

• A：关于原点对称
• B：关于x轴对称
• C：关于直线 y=1对称
• D：关于y轴对称

答 案：D

解 析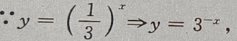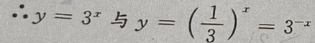：关于y轴对称，

主观题

1、弹簧的身长与下面所挂砝码的重量成正比，知弹簧挂20g重的砝码时长度是12cm,挂35g重的砝码时长度是15cm，写出弹簧长度y(cm)与砝码重x(g)的函数关系式，并求弹簧不挂砝码时的长度  

答 案：设弹簧原长为y0cm，则弹簧伸长量为（y-y0）cm。 由题意得 y-y0 =kx,即 y= kx+y0， 所求函数关系式为y=0.2x+8，弹簧的原长为8CM

2、已知函数f（x）=（x-4）（x2-a）。（I）求f’（x）；
（Ⅱ）若f’（-1）=8，求f（x）在区间[0，4]的最大值与最小值。

答 案：(I)f'(x) =(x-4)'(x²-a)+(x-4)(x²-a)’ =x²-a+2x(x-4) =3x²-8x-a. (Ⅱ)由于f’(-1)=3+8-a=8,得a=3. 令f'(x)=3x²-8x-3=0,解得x1=3，（舍去）又f（0）=12，f（3）=-6，f（4）=0所以在区间[0，4]上函数最大值为12，最小值为-6

3、设椭圆的中心是坐标原点,长轴在x轴上,离心率已知点P到圆上的点的最远距离是求椭圆的方程  

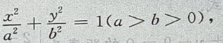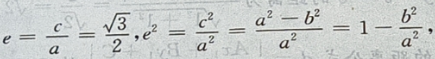
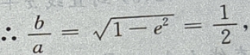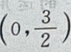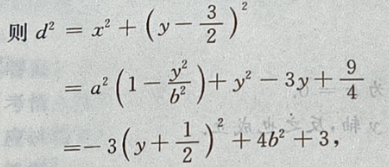
答 案：由题意，设椭圆方程为 由 设P点到椭圆上任一点的距离为 d, 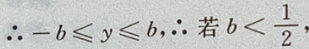则在y=-b时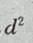，最大，即d也最大。  

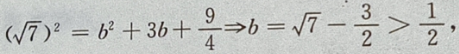
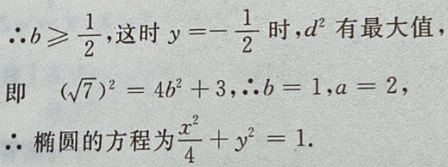
4、设函数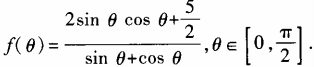 （1）求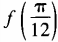；（2）求函数f（θ）最小值。

答 案：

填空题

1、“a=0，且b=0”是“a²+b²=0的”______。  

答 案：充要条件

2、直线的倾斜角的度数为（）  

答 案：60°

解 析：由题意知直线的斜率为设直线的倾斜角为α，则tanα=由0°≤α≤180°，故α=60°