2025年成考高起点《数学(理)》每日一练试题01月14日

2025年成考高起点《数学(理)》每日一练试题01月14日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、设A、B、C是三个随机事件,用A、B、C的运算关系（）表示事件:B、C都发生,而A不发生  

• A：
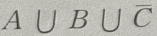
• B：
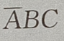
• C：
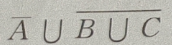
• D：

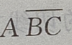
答 案：B

解 析：选项A,表示A或B发生或C不发生，选项C,表示A不发生或B、C不发生.选项D,表示A发生且 B、C 不发生.

2、14@@如图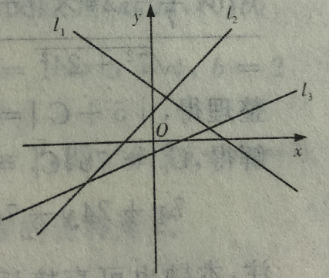，中直线l1、l2、l3的斜率分别为k1、k2、k3，则（）。

• A：k1
• B：k1
• C：k3
• D：k3

答 案：B

解 析：根据直线的位置、倾斜角，可得出斜率的大小关系，故选B。  

3、在点x＝0处的导数等于零的函数是（）。

• A：y＝sinx
• B：y＝x－1
• C：y＝ex－x
• D：y＝x²－x

答 案：C

解 析：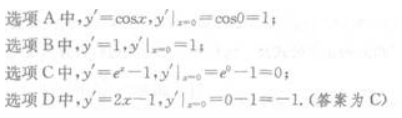

4、某类灯泡使用时数在1000小时以上的概率为0.2,三个灯泡在使用1000小时以后最多只有一个坏的概率为（）

• A：0.008
• B：0.104
• C：0.096
• D：1

答 案：B

解 析：已知灯泡使用1000小时后好的概率为0.2,坏的概率为1-0.2=0.8,则三个灯泡使用1000小时以后，可分别求得: P(没有坏的)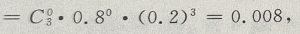 P(一个坏的)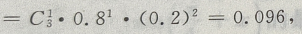故最多只有一个坏的概率为:0.008+0.096=0.104.  

主观题

1、已知数列的前n项和 求证：是等差数列，并求公差和首项。  

答 案：  

2、设分别讨论x→0及x→1时f（x）的极限是否存在？

答 案：∴f（x）在x=0处极限不存在 同理f（x）在x=1处极限存在

3、求下列函数的定义域： （1）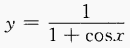
（2）
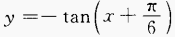
（3）  

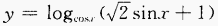
答 案：（1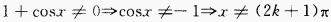） ∴函数的定义域为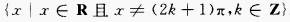（2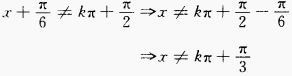） ∴函数的定义域为（3）
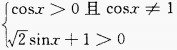
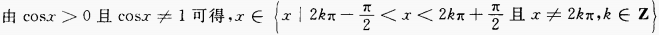
由对数函数的性质知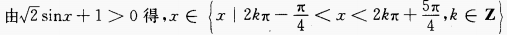， 故函数的定义域为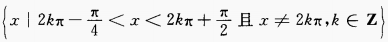  

4、计算 （1）tan5°+ cot5°- 2sec80°
（2）tan15°+cot15
（3）sin15°sin75°

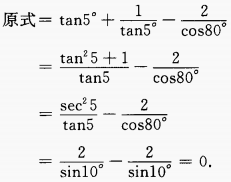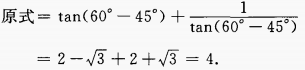答 案：（1）化切割为弦进行运算。 （2） （3）

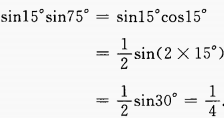
填空题

1、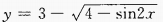的值域是______。  

答 案：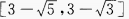

解 析：当sin2x=-1时，y最小值当 sin2x=1时,  

2、若tanα-cotα=1，则=______。

答 案：4

解 析：由立方差公式得,tan³α-cot³α=(tana-cotα)(tan²α+tanαcota+cot²α)(tana-cotα)[(tanα-cotα)²+3tanαcotα]=4