2025年成考高起点《数学(文史)》每日一练试题01月14日

2025年成考高起点《数学(文史)》每日一练试题01月14日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、与圆x²+y²=4关于点M(3，2)成中心对称的曲线方程是（　）  

• A：
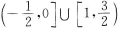
• B：
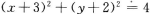
• C：
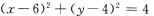
• D：

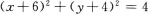
答 案：C

解 析：与圆关于点M成中心对称的曲线还是圆．只要求出圆心和半径，即可求出圆的方程．圆x²+y²=4的圆心(0，0)关于点M(3，2)成中心对称的点为(6，4)，所以所求圆的圆心为(6，4)，半径与对称圆的半径相等，所以所求圆的方程为(x-6)²+(y-4)²=4． 【考点指要】本题主要考查中心对称图形的定义、中点坐标公式的灵活运用、圆的标准方程的求法，这些主要概念在考试大纲中要求掌握，同时也是近几年经常考到的知识点．

2、已知b₁、b₂、b₃、b₄成等差数列，且b₁、b₄为方程2x²-3x+1=0的两个根，则b₂+b₃的值为（）。  

• A：1/2
• B：-3/2
• C：-1/2
• D：3/2

答 案：D

3、已知，则sin2α=（）

• A：
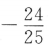
• B：
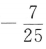
• C：
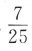
• D：

答 案：D

解 析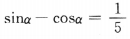：两边平方得，故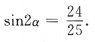

4、已知sinα+cosα=，sinα-cosα=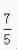，则tanα等于（）。

• A：
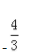
• B：
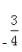
• C：1
• D：-1

答 案：A

主观题

1、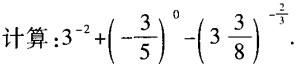  

答 案：

2、已知a^m=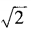，aⁿ=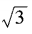，求a^3n-4m的值。  

答 案：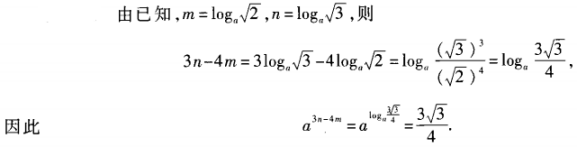

3、cos20°cos40°cos80°的值。  

答 案：

4、已知lg2=a，lg3=b，求lg0.15关于a，b的表达式。  

答 案：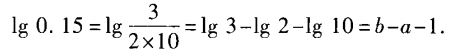

填空题

1、在等比数列中，a₁=3，a_n=96，S_n=189，则公比q=______，项数n=_______。  

答 案：q=2，n=6

解 析：解法一：An=A1×q^(n-1)=3q^(n-1)=96q^(n-1)=32S(n-1)=Sn-An=189-96=93
S(n-1)=A1×(1-q^(n-1))/(1-q)
=3(1-32)/(1-q)=93
q=2
2^(n-1)=32
n=6 解法二：  

2、函数f(x)=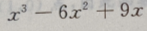在区间[-3,3]上的最大值为（）  

答 案：4

解 析：这题考的是高次函数的最值问题，可用导数来求函数在区间[-3,3]上的最值。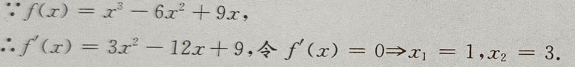 列出表格 由上表可知函数在[-3,3]上，在x=1点处有最大值为4.