2025年成考高起点《数学(理)》每日一练试题01月15日

2025年成考高起点《数学(理)》每日一练试题01月15日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

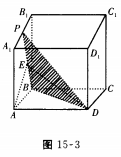
1、若P为正方体A1C中A1B1棱上的中点，则过P、B、D三点的平面与AA1B1B面所成的二面角的余弦值为（）。

• A：
• B：
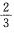
• C：
• D：

答 案：B

解 析：

2、下列四个命题中正确的是（）。 ①已知a，b，c三条直线，其中a，b异面，a//c，则b，c异面。
②若a与b异面，b与c异面，则a与c异面。
③过平面外一点与平面内一点的直线，和平面内不经过该点的直线是异面直线。
④不同在任何一个平面内的两条直线叫异面直线。

• A：③④
• B：②③④
• C：①②③④
• D：①②

答 案：A

解 析：①b与c可相交，②a与c可以有平行、相交、异面三种位置关系。答案为A。  

3、已知{i，j，k}是单位正交基底，a＝i＋j，b＝－i＋j－k，则a·b＝（）。

• A：-1
• B：1
• C：0
• D：2

答 案：C

解 析：a·b＝（1，1，0）·（－1，1，－1）＝1×（－1）＋1×1＋0×（－1）＝0。答案为C。  

4、函数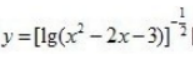定义域为（）。

• A：{x|x＜3,x∈R}
• B：{x|x＞-1.x∈R}
• C：{x|-1＜x＜3,x∈R}
• D：{x|＜-1或x＞3,x∈R}

答 案：D

主观题

1、求函数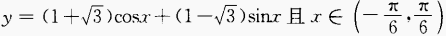上的最大值以及取得这个最大值的x。

答 案：.1 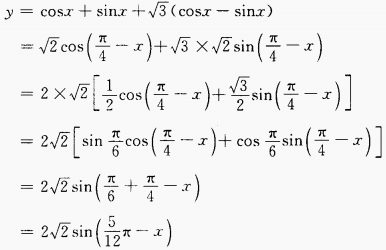函数取最大值，即y最大值=。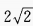

2、某气象预报站天气预报的准确率为80%，计算（1）5次预报中恰有4次准确的概率； （2）5次中至少有次准确的概率.(计算结果保留两个有效数字).  

答 案：  把每次预报看做一次试验，“预报结果准确”看成事件P（A）=0.8，本题就相当于在5次独立重复试验中求A恰好发生4次（或至少4次）的概率，此题属于独立重复试验，由公式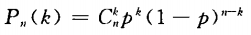来求解。 （1）n=5；p=0.8；k=4 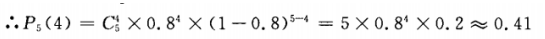即恰有4次准确的概率为0.41. (2)5次至少有4次准确的概率,就是5次中恰有4次准确的概率与5次预报中都准确的概率的和,即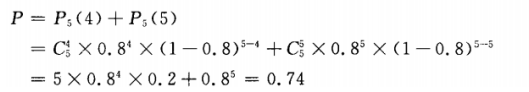 即至少有4次准确的概率为0.74。  

3、设分别讨论x→0及x→1时f（x）的极限是否存在？

答 案：∴f（x）在x=0处极限不存在 同理f（x）在x=1处极限存在

4、已知直线l的斜率为1，l过抛物线C：的焦点，且与C交于A,B两点.(I）求l与C的准线的交点坐标；
(II）求|AB|.

答 案：(I）C的焦点为，准线为由题意得l的方程为因此l与C的准线的交点坐标为(II）由，得设A（x1,y1），B（x2,y2），则因此

填空题

1、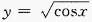的定义域是______。  

答 案：1

解 析：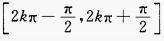

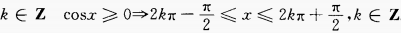
2、函数y=2cosx-cos2x（x∈R）的最大值为______。  

答 案：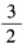

解 析：