2025年成考高起点《数学(理)》每日一练试题01月21日
2025-01-21 12:22:52 来源:人人学历网
2025年成考高起点《数学(理)》每日一练试题01月21日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、二次函数y=2x2+mx-5在区间(-∞,-1)内是减函数,在区间(-1,+∞)内是增函数,则m的值是()。
- A:4
- B:-4
- C:2
- D:-2
答 案:A
解 析:由题意可知二次函数y=2x2+mx-5的对称轴方程为x=-1,又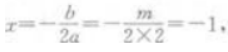 解得m=4
解得m=4
2、已知两条异面直线m;n,且m在平面α内,n在平面β内,设甲:m//β,n//α;乙:平面α//平面β,则()。
- A:甲为乙的必要但非充分条件
- B:甲为乙的充分但非必要条件
- C:甲非乙的充分也非必要条件
- D:甲为乙的充分必要条件
答 案:D
解 析:两条异面直线m,n,且m在平面α内,n在平面β内,因为m//β,n//α←→平面α∥平面β,则甲为乙的充分必要条件。答案为D。
3、若f(x+1)=x2-2x+3,则f(x)=()。
- A:x2+2x+6
- B:x2+4x+6
- C:x2-2x+6
- D:x2-4x+6
答 案:D
解 析:f(x+1)=x2-2x+3=(x+1)2-4(x+1)+6,∴f(x)=x2-4x+6。(答案为D)
4、(sinα+sinβ)2+(cosα+cosβ)2=()。
- A:
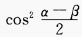
- B:
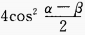
- C:
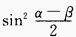
- D:
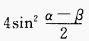
答 案:B
解 析: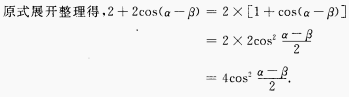
主观题
1、求下列函数的定义域: (1)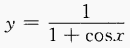
(2)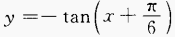
(3)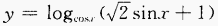
答 案:(1) 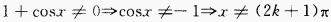 ∴函数的定义域为
∴函数的定义域为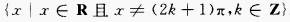 (2)
(2) 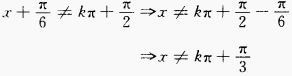 ∴函数的定义域为
∴函数的定义域为 (3)
(3)
由对数函数的性质知,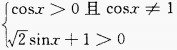
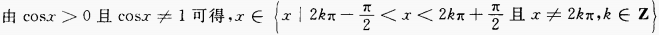
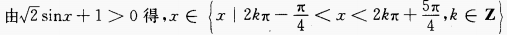 故函数的定义域为
故函数的定义域为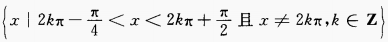
2、已知关于x的二次方程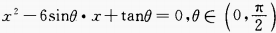 的两根相等,求sinθ+cosθ的值。
的两根相等,求sinθ+cosθ的值。
答 案:

3、求(1+tan10°)(1+tan35°)的值。
答 案:原式=1+tan10°+tan35°+tan10°·tan35°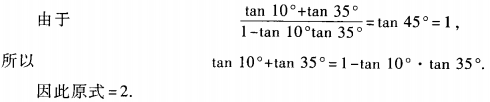
4、设函数f(x)= (Ⅰ)求f(x)的单调区间;
(Ⅱ)求 f(x)的极值
(Ⅰ)求f(x)的单调区间;
(Ⅱ)求 f(x)的极值
答 案:(Ⅰ)函数的定义域为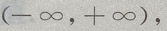
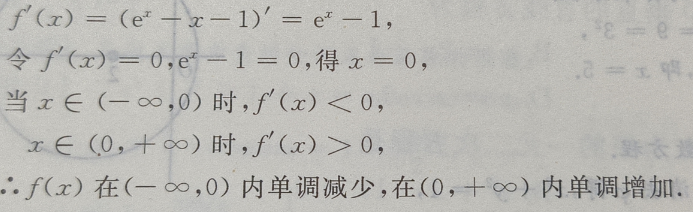 (Ⅱ)
(Ⅱ)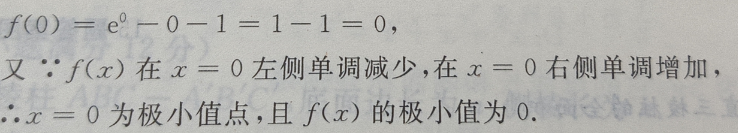
填空题
1、与已知直线 7x+24y-5 =0 平行,且距离等于3的直线方程是______。
答 案:7x+24y+70=0或7z+24y-80-0
解 析:
2、已知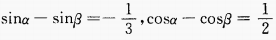 ,则
,则 =______。
=______。
答 案: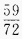
解 析: