2025年成考高起点《数学(文史)》每日一练试题01月22日

2025年成考高起点《数学(文史)》每日一练试题01月22日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、若向量a=（x，2），b=（-2，4），且a⊥b，则x=（）。

• A：-4
• B：-1
• C：1
• D：4

答 案：D

2、甲、乙两个人各进行一次射击，甲击中目标的概率是0.2，乙击中目标的概率是0.7，则甲、乙两人都击中目标的概率是（）。

答 案：A

解 析：本题属于相互独立事件同时发生的概率，设A为甲击中目标的事件，B为乙击中目标的事件，P（A）=O.2，P（B）=0.7，P（A·B）=P（A）·P（B）=O.2×0.7=0.14，故应选A。

3、若-1，a,b,c,-9五个数列成等比数列，则（）

• A：b=3,ac=9
• B：b=-3,ac=9
• C：b=-3,ac=-9
• D：b=3,ac=-9

答 案：B

解 析：因为-1，a,b,c,-9成等比数列，所以ac=b2=-1×(-9)=9,所以ac=9，b=±3，又因为-1，a,b成等比数列，所以a2=-b＞0，所以b=-3  

4、已知点M(-2,5),N(4,2),点P在上，且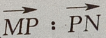=1:2，则点P的坐标为（）

• A：
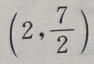
• B：(0,4)
• C：(8,2)
• D：(2,1)

答 案：B

解 析：由题意得：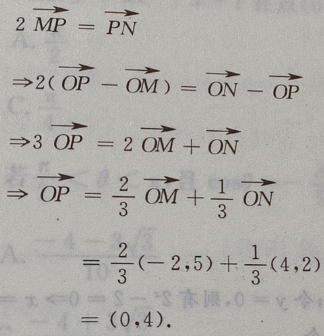  

主观题

1、如图：已知在△ADC中，∠C=90°，∠D=30°，∠ABC=45°，BD=20，求AC(用小数表示，保留一位小数)  

答 案：如图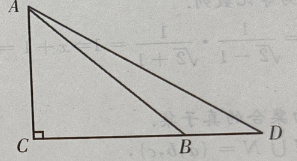  

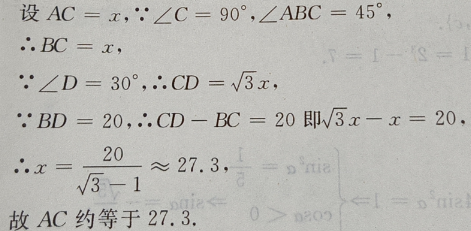
2、已知F是椭圆的右焦点，点M在抛物线y2=2px（p＞0）上O为坐标原点，且△MOF为正三角形．  (Ⅰ)求P的值； (Ⅱ)求抛物线的焦点坐标和准线方程．

答 案：(Ⅰ)由椭圆方程可知，椭圆的长半轴a=5，短半轴，则椭圆的半焦距 即椭圆的右焦点F的坐标为 (4.0). 如图,因为△MOF为正三角形,OF=4,过M作MN⊥OF于N点， 【考点指要】本题主要考查椭圆、抛物线的概念，要求考生掌握它们的标准方程和性质，会用它们解决有关的问题．  

3、设3^a=5^b=15，求a^-1+b^-1的值。  

答 案：由3^a=15，得a=log₃15；又由5^b=15，得b=log₅15。 因此a^-1+b^-1=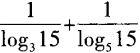 =log₁₅3+log₁₅5=1。

解 析：过程中应用了换底公式的推论，即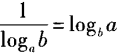

4、在△ABC中，AB=2，BC=3,B=60°，求AC及△ABC的面积

答 案：

填空题

1、“a＞b”是“a-c＞b-c”的______。

答 案：充要条件

2、设直线y=2x+m与抛物线y²=4x没有公共点，则m的取值范围是______。  

答 案：