2025年成考高起点《数学(文史)》每日一练试题01月29日

2025年成考高起点《数学(文史)》每日一练试题01月29日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、掷两颗骰子点数之和等于4的概率是（）。

• A：
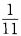
• B：
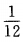
• C：
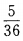
• D：

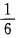
答 案：B

解 析：掷一对骰子的等可能结果共有n=36种，点数之和等于4的结果有1+3=4，3+1=4，2+2=4，故有m=3种，所以其概率为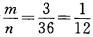故选B。  

2、若|a|=1，|b|=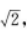（a-b）⊥a，则a与b的夹角为（　）

• A：30°
• B：45°
• C：60°
• D：75°

答 案：B

解 析：因为(a-b)⊥a， 【考点指要】本题考查向量的模与夹角的计算、向量的数量积的几何意义及对垂直问题的应用

3、如果方程lg2x+(lg2+lg3)lgx+lg2×lg3=0的两个根分别是x1，x2，那么x1·x2=（　）

• A：lg2×lg3
• B：lg2+lg3
• C：1/6
• D：-6

答 案：C

解 析：【考点指要】本题考查一元二次方程的有关知识及对数的运算法则．注意此方程不是关于2的二次方程，是关于lgx的二次方程，因此运用韦达定理时需要写成lgx1+lgx2与lgx1·lgx2，最好采用题解中换元的方法．

4、已知向量a=(3,4),b=(0,-2),则cos=()  

• A：
• B：
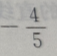
• C：
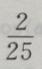
• D：

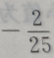
答 案：B

解 析：因为a=(3,4),b=(0,-2),  

主观题

1、每亩地种果树20棵时,每棵果树收入90元,如果每亩增种一棵,每棵果树收入就下降3元,求使总收入最大的种植棵数.  

答 案：设每亩增种x棵,总收入味y元，则每亩种树(20+x)棵，由题意知增种x棵后每棵收入为（60-3x） 则有y=(90-3x)(20+x) 整理得y=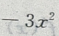+30x+1800 配方得y=+1875 当x=5时，y有最大值，所以每亩地最多种25棵

2、已知函数ƒ(x)=ax3-x2+bx+1(a，b∈R)在区间(-∞，0)和(1，+∞)上都是增函数，在(0，1)内是减函数． (Ⅰ)求a，b的值； (Ⅱ)求曲线y=ƒ(x)在x=3处的切线方程．

答 案：(Ⅰ)因为函数ƒ(x)在(-∞，0)上递增，在（0,1）内递减，在（1，+∞）上有递增，可知函数在x=0和x=1处的导数值均为0. 又f’(x)=3ax²-2x+b, 所以f’(0)=b=0,f’(1)=3a-2+b=0. 即切点为(3.10),所以其切线方程为y-10=12(x-3),即12x-y-26 = 0.  

解 析：【考点指要】本题主要考查函数导数的几何意义、导数的求法和导数的应用——函数的单调区间及曲线的切线方程的求法  

3、（1）已知tanα=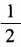 求cot2α的值； （2）已知tan2α=1，求tanα的值。

答 案：（1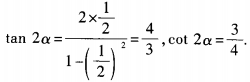） （2）由已知，得 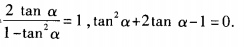解关于tanα的一元二次方程，得tanα=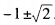

4、已知a^m=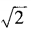，aⁿ=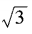，求a^3n-4m的值。  

答 案：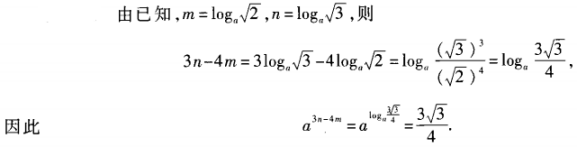

填空题

1、与已知直线7x+24y-5=0平行，且距离等于3的直线方程是______。  

答 案：7x+24y+70=0或7x+24y-80=0

解 析：设要求的直线方程为7x+24y+c=0， ∵直线7x+24y+c=0到直线7x+24y-5=0的距离等于3 ∴ ∴.C=70或-80. 故所求的直线方程为7x+24y+70=0或7x+24y-80=0

2、一个问题在1小时内，甲能独立解决的概率是0.5，乙能独立解决的概率是0.4，两人在1小时内解决问题的概率是______。

答 案：0.7