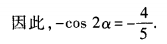2025年成考高起点《数学(文史)》每日一练试题02月04日
2025-02-04 12:18:49 来源:人人学历网
2025年成考高起点《数学(文史)》每日一练试题02月04日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、甲袋内有2个白球3个黑球,乙袋内有3个白球1个黑球,现从两个袋内各摸出1个球,摸出的两个球都是白球的概率是
- A:

- B:
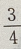
- C:

- D:
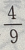
答 案:C
解 析:由已知条件可知此题属于相互独立同时发生的事件,从甲袋内摸到白球的概率为P(A)=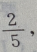 乙袋内摸到白球的概率为
乙袋内摸到白球的概率为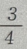 ,所以现从两袋中各提出一个球,摸出的两个都是白球的概率为
,所以现从两袋中各提出一个球,摸出的两个都是白球的概率为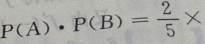
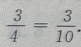
2、已知集合A={0,1,2,3,4},B={x|0<x<4},则A∩B=()。
- A:{0,1,2,3}
- B:{1,2,3}
- C:{1,2}
- D:{0,4}
答 案:B
3、设f(x)=x3+4x2+11x+7,则f(x+1)=()。
- A:x3+7x2+22x+23
- B:x3—7x2+22x+23
- C:x3+7x2-22x+23
- D:x3-7x2-22x+23
答 案:A
解 析:f(x+1) =(x+1)3 +4(x+1}2+11(x+1)+7 =x3+3x2+3x+1+4x2+8x+4+11x+11+7 =x3+7x2+22x+23 综上所述,答案:x3+7x2+22x+23
4、已知sinα= 且
且 ,则tanα的值等于()。
,则tanα的值等于()。
- A:

- B:

- C:

- D:

答 案:D
主观题
1、如图:已知在△ADC中,∠C=90°,∠D=30°,∠ABC=45°,BD=20,求AC(用小数表示,保留一位小数)

答 案:如图 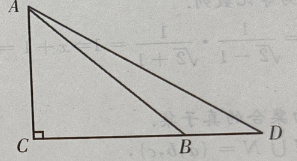
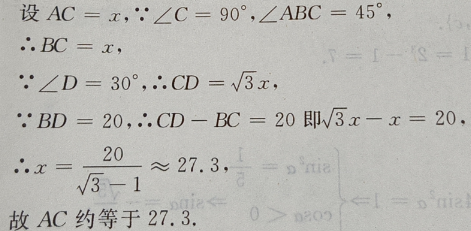
2、已知a,b,c成等比数列,x是a,b的等差中项,y是b,c的等差中项证明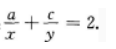
答 案: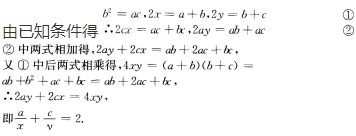 考点 本题考查考生对等差中项和等比中项公式的理解及运用.
考点 本题考查考生对等差中项和等比中项公式的理解及运用.
3、求函数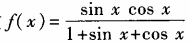 (x∈R)的最大值与最小值。
(x∈R)的最大值与最小值。
答 案:设sinx+cosx=t,则(sinx+cosx)2=t2,1+2sinxcosx=t2,sinxcosx= 于是转化为求
于是转化为求 的最值。
由所设知
的最值。
由所设知 上为增函数,故g(t)的最大值为
上为增函数,故g(t)的最大值为 最小值为
最小值为
4、设函数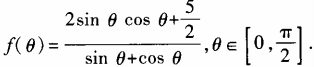 (1)求
(1)求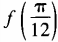 ;(2)求函数f(θ)最小值。
;(2)求函数f(θ)最小值。
答 案:
填空题
1、平面内有10个点,任何三点都不在同一直线上,问能连成______条不同的直线。
答 案:45
2、已知点P(-3,1)为角α终边上一点,则cos(2α-π)的值等于______。
答 案: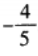
解 析:因为cos(2α-π)=cos(π-2α)=-cos2α。由已知,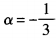 所以
所以