2025年成考高起点《数学(文史)》每日一练试题03月31日
2025-03-31 12:27:42 来源:人人学历网
2025年成考高起点《数学(文史)》每日一练试题03月31日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、已知b1、b2、b3、b4成等差数列,且b1、b4为方程2x2-3x+1=0的两个根,则b2+b3的值为()。
- A:1/2
- B:-3/2
- C:-1/2
- D:3/2
答 案:D
2、函数f(x)=x3-6x2+9x-3的单调区间为()。
- A:(-∞,-3),(-3,1),(1,+∞)
- B:(-∞,-1),(-1,3),(3,+∞)
- C:(-∞,-3),(-3,-1),(-1,+∞)
- D:(-∞,1),(1,3),(3,+∞)
答 案:D
解 析:∵x∈R
f’(x)=3x2-12x+9
=3(x2-4x+3)
=3(x-3)(x-1)
∴x>3或x<1,f’(x)>0,
1 3、在自然数1、2、…、100中任取一个数能被3整除的概率是()。 答 案:C 解 析:此题属于等可能事件的概率,n=100,m=33,其概率为 4、设 答 案:A 主观题 1、已知等差数列 答 案:(Ⅰ)当n=1时,由 2、如图9-4,已知测速站P到公路L的距离为40米,一辆汽车在公路L上行驶,测得此车从A点行驶到8点所用的时间为2秒,并测得∠APO=60°,∠BPO=30°,计算此车从A到B的平均速度为多少km/h(结果保留到个位),并判断此车是否超过了80km/h的限制速度。
答 案:此车从A到B的平均速度为83(km/h),已经超过80km/h的限制速度。 3、已知a,b,c成等比数列,x是a,b的等差中项,y是b,c的等差中项证明 答 案: 4、教室里有50人在开会,其中学生35人,家长12人,老师3人,现校长在门外听到有人在发言,那么发言人是老师或学生的概率为多少?
答 案:此题属于互斥事件,发言人是老师的概率为 填空题 1、函数y=-x²+ax图像的对称轴为x=2,则a=______。 答 案:4
解 析:本题主要考查的知识点为二次函数的性质。 由题意,该函数图像的对称轴为 2、在∆ABC中,已知cosA= 答 案: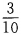
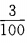
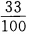
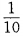
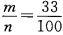 ,故应选C。
,故应选C。
 <1,则a的取值范围是()。
<1,则a的取值范围是()。



 前n项和
前n项和 (Ⅰ)求通项
(Ⅰ)求通项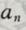 的表达式
(Ⅱ)求
的表达式
(Ⅱ)求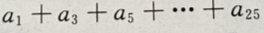 的值
的值
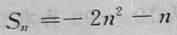 得
得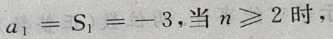
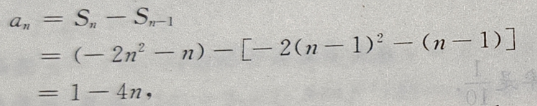
 也满足上式,故
也满足上式,故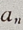 =1-4n(n≥1)
(Ⅱ)由于数列
=1-4n(n≥1)
(Ⅱ)由于数列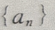 是首项为
是首项为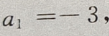 公差为d=-4的等差数列,所以
公差为d=-4的等差数列,所以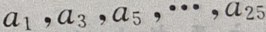 是首项为
是首项为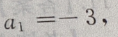 公差为d=-8,项数为13的等差数列,于是由等差数列前n项和公式得:
公差为d=-8,项数为13的等差数列,于是由等差数列前n项和公式得:

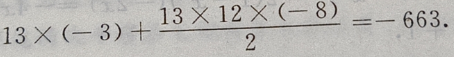

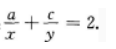
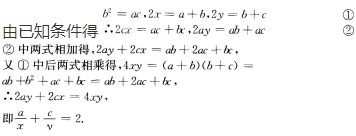 考点 本题考查考生对等差中项和等比中项公式的理解及运用.
考点 本题考查考生对等差中项和等比中项公式的理解及运用.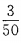 ,是学生的概率为
,是学生的概率为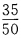 ,故所求概率为。
,故所求概率为。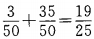
 得a=4。
得a=4。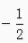 ,cosB=
,cosB=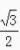 ,那么cosC=______。
,那么cosC=______。
2023年成考高起点《数学(文史)》每日一练试题03月31日 03-31 2024年成考高起点《数学(文史)》每日一练试题03月31日 03-31 2025年成考高起点《数学(文史)》每日一练试题01月31日 01-31 2025年成考高起点《数学(文史)》每日一练试题03月03日 03-03 2025年成考高起点《数学(文史)》每日一练试题03月19日 03-19 2025年成考高起点《数学(文史)》每日一练试题03月20日 03-20 2025年成考高起点《数学(文史)》每日一练试题03月21日 03-21 2025年成考高起点《数学(文史)》每日一练试题03月22日 03-22



