2025年成考高起点《数学(理)》每日一练试题06月09日

2025年成考高起点《数学(理)》每日一练试题06月09日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、=（）。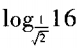

• A：8
• B：-8
• C：2
• D：-2

答 案：B

解 析：由于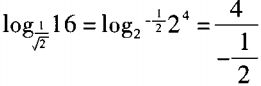。log2²=-8。故选B。

2、袋中有6个球，其中4个红球，2个白球，从中随机取出2个球，则其中恰有1个红球的概率为（）

• A：
• B：
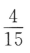
• C：
• D：

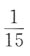
答 案：A

解 析：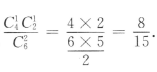

3、已知正三棱柱的底面积等于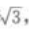侧面积等于30,则此正三棱柱的体积为（）。

• A：
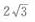
• B：
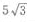
• C：
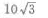
• D：

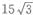
答 案：B

解 析：设正三梭柱的底面的边长为a,底面积为 设正三棱柱的高为h,侧面积为3×a×h=3×2×h=30,得h=5.则此正三棱柱的体积为底面积×高=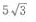

4、设f(x)=x³+ax²+x为奇函数，则a=（）。

• A：1
• B：0
• C：
• D：-2 D.C.-1

答 案：B

解 析：本题主要考查的知识点为函数的奇偶性. 因为f(x)为奇函数，故f(-x)=-f(x)。即-x³+ax²-x=-x³-ax²-x，a=0。

主观题

1、（1）已知tanα=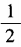，求cot2α的值； （2）已知tan2α=1，求tanα的值。

答 案：（1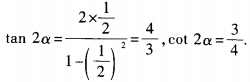）（2）由已知，得 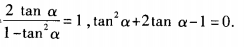解关于tanα的一元二次方程，得tanα=  

2、在△ABC中，B=120°,BC=4,△ABC的面积为，求AC.

答 案：由△ABC的面积为得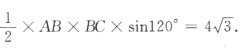所以AB =4.因此所以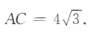

3、已知A（1，4），B（3，8），C（4，10）。求证A、B、C三点共线。  

答 案：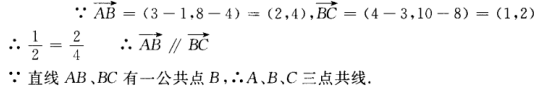

4、空间有四个点，如果其中任何三点不在同一直线上，可以确定几个平面?  

答 案：根据公理，在所给定的四点中任取三点，可确定一个平面，由组合公式所以共可确定四个平面。

解 析：空间有n个点，如果其中任何三点不在同一直线上，可以确定个平面。  

填空题

1、y=lg（sinx）的定义域是______。  

答 案：2kπ＜x＜(2k+1)π(k∈Z)

解 析：sinx＞0∴x属于第一、二象限,所以 2kπ＜x＜(2k+1)π(k∈Z)

2、化简sin（x+y）-2cosxsiny=______.  

答 案：sin（x-y）

解 析：原式=sinxcosy+cosxsiny-2cosxsiny=sinxcosy-cosxsiny=sin（x-y）