2024年成考专升本《高等数学一》每日一练试题12月14日
2024-12-14 11:31:40 来源：人人学历网
2024年成考专升本《高等数学一》每日一练试题12月14日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。
单选题
1、函数z＝f(x,y)在点P(x,y)处的偏导数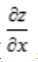
，
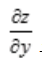为连续函数，是函数z＝f(x,y)在点P(x,y)处可微分的（）。
- A：充分条件
- B：必要条件
- C：充分必要条件
- D：既非充分也非必要条件
答 案：A
解 析：由多元函数微分的充分条件可知，函数z＝f(x,y)在点P(x,y)处的偏导数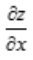
，
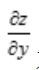为连续函数，是函数z＝f(x,y)在点P(x,y)处可微分的充分条件。
2、
（）。
- A：0
- B：1
- C：
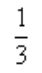
- D：
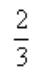
答 案：D
解 析：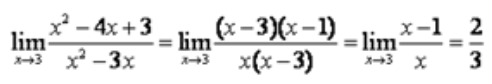
。
3、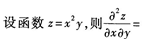
（）。
- A：x+y
- B：x
- C：y
- D：2x
答 案：D
解 析：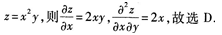
主观题
1、求
答 案：解：用洛必达法则，得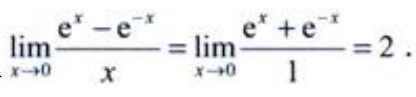
2、求y＝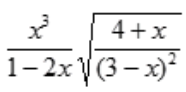
的一阶导数y'。
答 案：解：两边取对数得
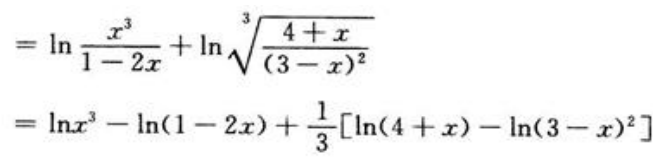两边对x求导得
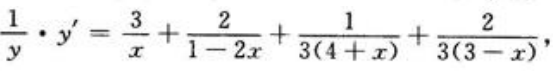故
3、设z＝x2y—xy3，求
答 案：解：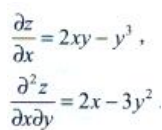
填空题
1、幂级数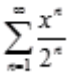
的收敛区间（不考虑端点）是（）。
答 案：（－2，2）
解 析：
，因此R＝
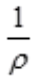＝2，所以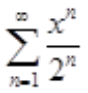
的收敛区间为（－2，2）。
2、过点M0（1，0，-1）且与直线垂直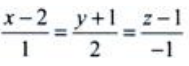
的平面方程为（）。
答 案：
解 析：所求平面与已知直线垂直，则平面的法线向量n必定与直线的方向向量s＝（1，2，－1）平行，可取n＝（1，2，－1），又平面过点（1，0，－1），由平面的点法式方程可知所求平面方程为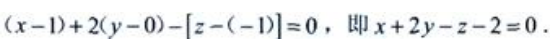
3、微分方程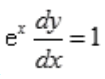
的通解为（）。
答 案：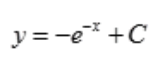
解 析：方程可化为：
，是变量可分离的方程，对两边积分即可得通解。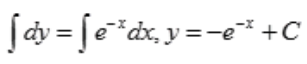
。
简答题
1、计算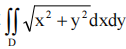
，其中D是由曲线
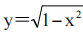，y＝x，y＝-x所围成的闭区域.
答 案：积分区域用极坐标可表示为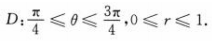
故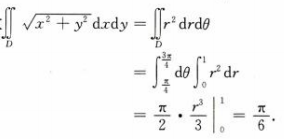
温馨提示：因考试政策、内容不断变化与调整，本站提供的以上信息仅供参考，如有异议，请考生以权威部门公布的内容为准！
- 备考交流
-
2025成考内部交流群群号：665429327
扫一扫或点击二维码入群
热门资讯
猜你喜欢
换一换
山东省2025年上半年高等学历继续教育学士学位外语考试报名时间
01-03
河南财经政法大学2025年成人本科学士学位申请时间安排
01-03
重庆成考报名时间2024具体时间
01-03
新疆成考报名时间2023 新疆成人高考什么时候报名
01-26
吉林成考报名时间2023具体时间
01-26
河南2023年成人高考考试科目及时间安排
01-26
2023年成人高考考试时间 2023年成考考试时间
01-26
2022年成人高考录取结果查询入口(全国各省汇总)
01-26
