2025年成考专升本《高等数学一》每日一练试题01月14日

2025年成考专升本《高等数学一》每日一练试题01月14日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、函数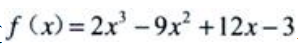单调减少的区间为（）。

• A：（－∞，1]
• B：[1，2]
• C：[2，＋∞）
• D：[1，＋∞）

答 案：B

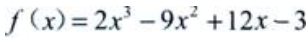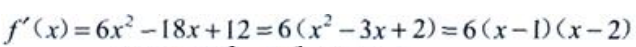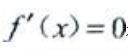解 析：的定义域为（－∞，＋∞），求导得令得驻点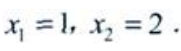当x＜1时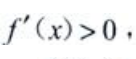，f（x）单调增加；当1＜x＜2时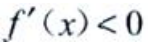，，f（x）单调减少；当x＞2时，f（x）单调增加.故单调递减区间为[1，2]。

2、（）。

• A：＞0
• B：＜0
• C：＝0
• D：不存在

答 案：C

解 析：被积函数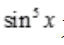为奇函数，且积分区间[1，1]为对称区间，由定积分的对称性质知该函数的积分为0。

3、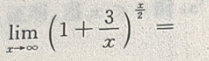  

• A：
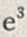
• B：
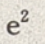
• C：
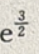
• D：

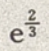
答 案：C

解 析：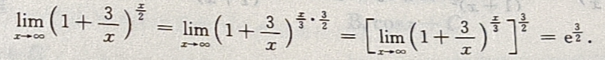

主观题

1、试证：当x＞0时，有不等式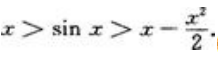

答 案：证：先证x＞sinx（x＞0）。设f（x）＝x－sinx，则f（x）＝1－cosx≥0（x＞0），所以f（x）为单调递增函数，于是对x＞0有f（x）＞f（0）＝0，即x－sinx＞0，亦即x＞sinx（x＞0）。再证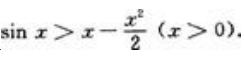
令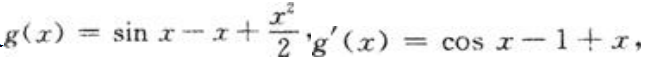
则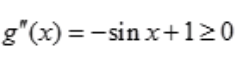，所以g'(x)单调递增，又g'(x)＝0，可知g'(x)＞g'(0)＝0（x＞0），那么有g（x）单调递增，又g（0）＝0，可知g（x）＞g（0）＝0（x＞0），所以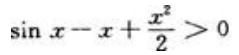即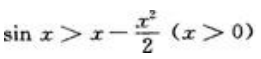
综上可得：当x＞0时，。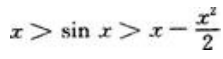

2、设z＝f（x，y）是由方程所确定，求。

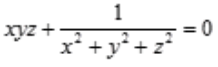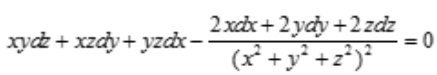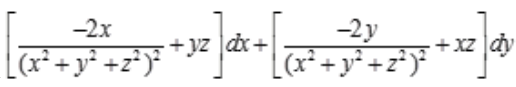
答 案：解：由得全微分方程：化简得所以。

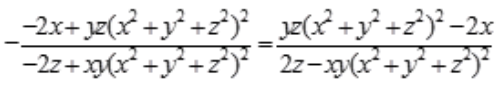3、在曲线上求一点M₀，使得如图中阴影部分的面积S₁与S₂之和S最小。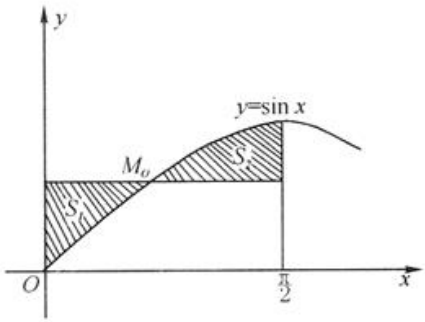

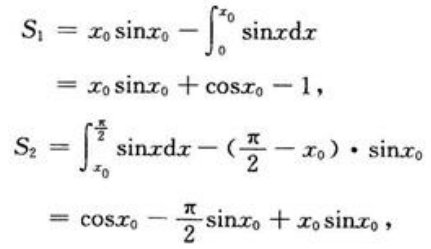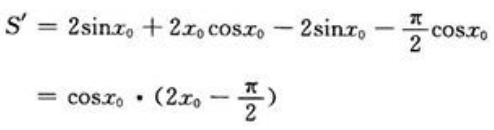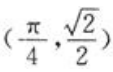答 案：解：设点M₀的横坐标为x₀，则有则S为x₀的函数，将上式对x₀求导得令S'=0,得，所以由于只有唯一的驻点，所以则点M₀的坐标为为所求。

填空题

1、过点(1,0,-1)与平面3x-y-z-2=0平行的平面的方程为（）

答 案：3x-y-z-4=0

解 析：平面3x-y-z-2=0的法向量为(3，-1，-1)，所求平面与其平行，故所求的平面的法向量为(3，-1，-1)，由平面的点法式方程得所求平面方程为3(x-1)-(y-0)-(z+1)=0，及3x-y-z-4=0。

2、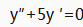的特征方程为________。  

答 案：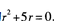

解 析：由特征方程的定义可知，所给方程的特征方程为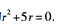

3、设函数z=ln（x+y²），则全微分dz=_______.  

答 案：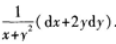

解 析：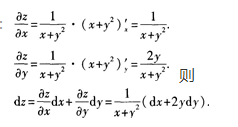

简答题

1、  

答 案：