2025年成考专升本《高等数学二》每日一练试题01月26日
2025-01-26 11:35:28 来源：人人学历网
2025年成考专升本《高等数学二》每日一练试题01月26日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考专升本每日一练的积累，助力我们更容易取得最后的成功。
判断题
1、若
，则
。（）
答 案：错
解 析：
所以
单选题
1、设函数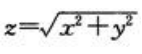
，则下列结论正确的是（）.
- A：
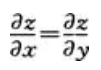
- B：
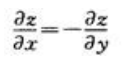
- C：
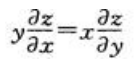
- D：
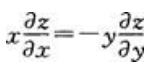
答 案：C
解 析：由函数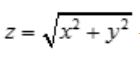
可计算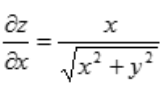
，
.
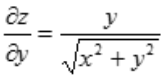2、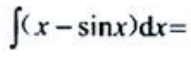
（）.
- A：x2＋cosx＋C
- B：
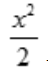＋cosx＋C - C：x2－sinx＋C
- D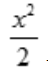：－sinx＋C
答 案：B
解 析：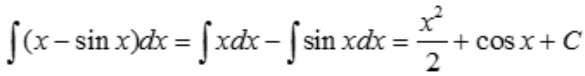
.
主观题
1、在半径为R的半圆内作一内接矩形，其中的一边在直径上，另外两个顶点在圆周上（如图所示）．当矩形的长和宽各为多少时矩形面积最大？最大值是多少？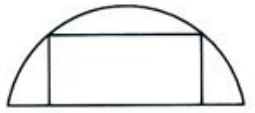
答 案：解：如图所示
，设x轴通过半圆的直径，y轴垂直且平分直径．设OA＝x，则AB＝
，矩形面积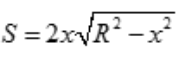
．
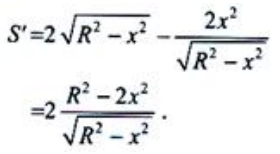令s'=0，得
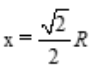（舍去负值）．
由于只有唯一驻点，根据实际问题x＝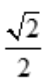
，必为所求，则AB＝
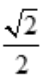R．所以，当矩形的长为
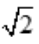R、宽为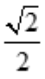
R时，矩形面积最大，且最大值S＝R2．
2、求二元函数f(x,y)＝x2＋y2＋xy在条件x＋2y＝4下的极值．
答 案：解：设
令
由式（1）与式（2）消去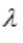
得x＝0，代入式（3）得y＝2．所以函数f(x,y)的条件极值为4．
填空题
1、设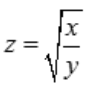
，则dz＝（）
答 案：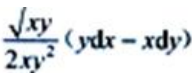
解 析：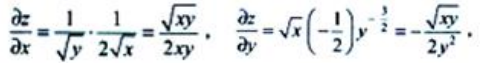
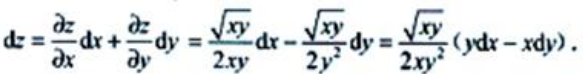
2、设
则y'=（）
答 案：
解 析：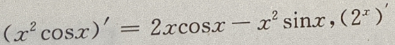
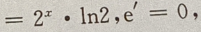所以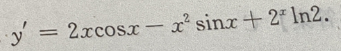
简答题
1、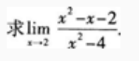
答 案：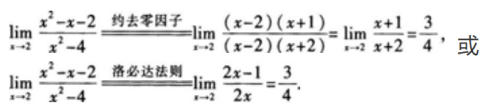
2、已知函数f（x）=ax3+bx2+cx在点x0处取得极大值5，其导函数y=f’（x）的图像经过点（1，0）和（2，0）（如图2-1-1所示）。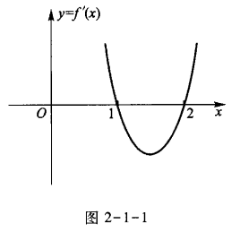
（1）求极值点x0的值；
（2）求a，b，c的值。
答 案：本题考查的知识点是利用导数的图像来判定函数的单调区间和极值点，并以此确定函数的表达式。 （1）在x=1处f’（1）=0，且x＜1时，f’（x）＞0；1＜x＜2时，f’（x）＜0，可知x=1是极值点，即x0=1。（2）因为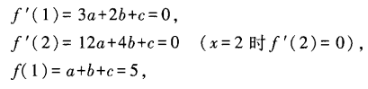
由上面三式解得a=2，b=-9，c=12。
- 备考交流
-
2025成考内部交流群群号：665429327
扫一扫或点击二维码入群
