2023年成考专升本《高等数学二》每日一练试题05月26日
2023-05-26 10:44:56 来源:人人学历网
2023年成考专升本《高等数学二》每日一练试题05月26日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考专升本每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、函数y=x+cosx在(0,2π)内()
- A:单调增加
- B:单调减少
- C:不单调
- D:不连续
答 案:A
解 析:由y=x+cosx,所以y'在1-sinx≥0(0 2、设 答 案:A 解 析:因为 3、设函数z=x2y3,则 答 案:A 解 析: 主观题 1、求由方程siny+xey=0确定的曲线在点(0,π)处的切线方程. 答 案:解:方程两边对x求导得 2、在抛物线y=1-x2与x轴所组成的平面区域内,做一内接矩形ABCD,其一条边AB在x轴上(如图所示) 答 案:解:(1) 3、求函数f(x,y)=x2+y2在条件2x+3y=1下的极值. 答 案:解:求条件极值,作拉普拉斯辅助函数F(x,y,λ)=f(x,y)+λ(2x+3y-1) 填空题 1、设y=y(x)是由方程 答 案: 解 析:因为 2、设函数 答 案:2 解 析:因为函数在x=0处连续,故有 3、若点(1,3)是曲线y=ax3+bx3拐点,则a,b分别为().
答 案: 解 析:因点(1,3)在曲线 简答题 1、计算 答 案: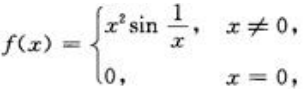 则f(x)在点x=0处().
则f(x)在点x=0处(). =0
=0 =1
=1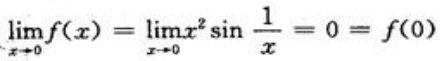 ,所以,f(x)在x=0处连续;又
,所以,f(x)在x=0处连续;又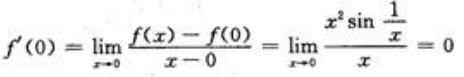 所以f(x)在点x=0处可导且
所以f(x)在点x=0处可导且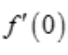 =0.
=0.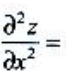 ().
().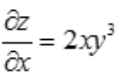 ,
,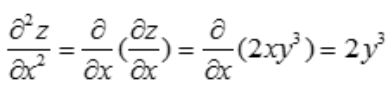 .
.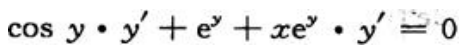 得
得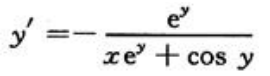 所以
所以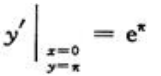 ,故所求切线方程为y-π=eπ(x-0),即eπx-y+π=0
,故所求切线方程为y-π=eπ(x-0),即eπx-y+π=0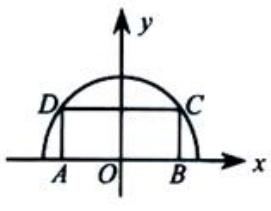 .设AB长为2x,矩形面积为S(x). (1)写出S(x)的表达式;
.设AB长为2x,矩形面积为S(x). (1)写出S(x)的表达式;
(2)求S(x)的最大值.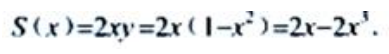
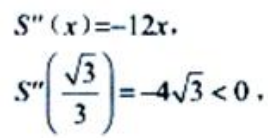 (2)
(2)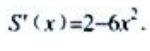 令
令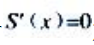 解得
解得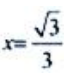 (
(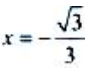 舍去)。则
舍去)。则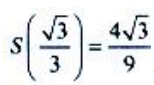 为极大值.由于驻点唯一,且实际问题有最大值,所以
为极大值.由于驻点唯一,且实际问题有最大值,所以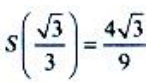 为最大值.
为最大值.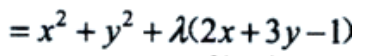 令
令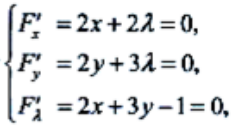 得
得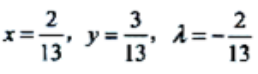 .
.
因此,f(x,y)在条件2x+3y=1下的极值为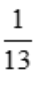 .
.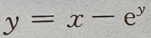 所确定的隐函数,则
所确定的隐函数,则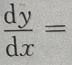 ()
()
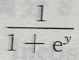
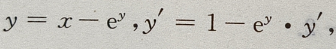 即
即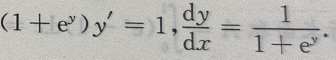
 ,在x=0处连续,则a=().
,在x=0处连续,则a=().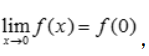 由于
由于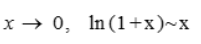
 所以a=2.
所以a=2.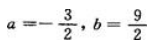
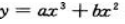 上,所以a+b=3.又因
上,所以a+b=3.又因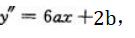 所以6a+2b=0.解方程组
所以6a+2b=0.解方程组