2024年高职单招《数学(中职)》每日一练试题12月06日
2024-12-06 16:02:48 来源：人人学历网
2024年高职单招《数学(中职)》每日一练试题12月06日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。
单选题
1、设t=a-4b,s=a+b²+4,则t与s的大小关系是（）
- A：s≥t
- B：s>t
- C：s≤t
- D：s
答 案：A
解 析：因为t=a-4b,s=a+b²+4,所以s-t=a+b²+4-(a-4b)=b²+4b+4=(b+2)²≥0,所以s≥t.
2、已知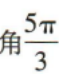
的顶点与坐标原点重合，始边与x轴正半轴重合，则角
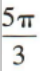的终边在（）
- A：第一象限
- B：第二象限
- C：第三象限
- D：第四象限
答 案：D
解 析：
3、函数y=cos2x的单调递减区间是（）
- A：
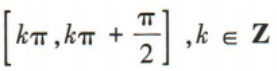
- B：
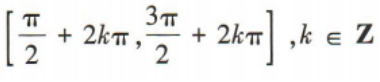
- C：
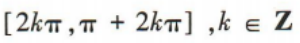
- D：
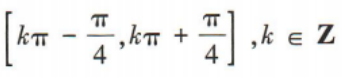
答 案：A
解 析：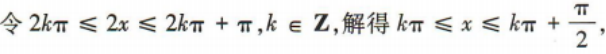
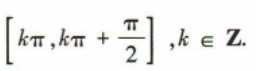
4、下列结论正确的是()
- A：
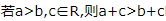
- B：
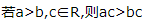
- C：
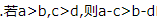
- D：
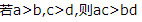
答 案：A
解 析：在不等式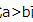
两边同时加上同一个数c,不等号的方向不变，所以
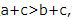,故A正确.当c=0时，ac=bc,故B错误.当a=2,b=1,c=3,d=0时，
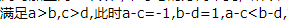故C错误.当a=1,b=0,c=0,d=-1时，满足
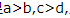此时ac=bd,故D错误.
填空题
1、(1+x)5的展开式中,二项式系数的和是()
答 案：32
解 析：令x=1,得二项式系数的和为25= 32.
2、已知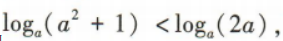
,则实数a的取值范围是（）
答 案：(0,1)
解 析：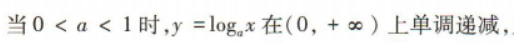
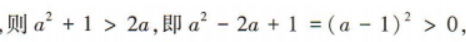
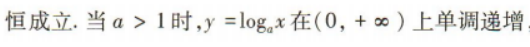
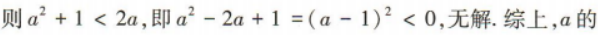
3、若f(x)为定义在R上的奇函数，则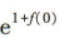
=（）
答 案：e
解 析：因为f(x)是定义在R上的奇函数，所以f(0)=0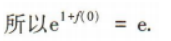
4、若角α的顶点与坐标原点重合，始边与x轴非负半轴重合，终边经过点(1,1),则sinα=（）
答 案：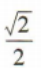
解 析：
简答题
1、已知向量a=(1,m),b=(2,3). (1)若a//b,求m的值； (2)若a⊥b,求3a·(b-3a)的值.
答 案：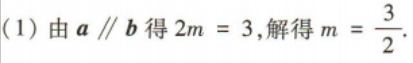
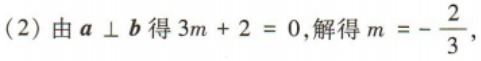
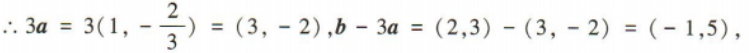
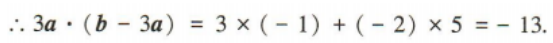
2、已知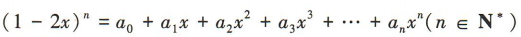
,该展开式的二项式系数之和为 32. (1)求n的值;(2)求
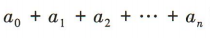的值.
答 案：(1)因为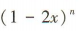
的展开式的二项式系数之和为 32, 所以2n=32,解得n=5.
(2)令x=1,得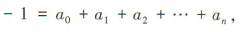
所以
- 备考交流
-
单招真题交流3群
扫一扫或点击二维码入群
