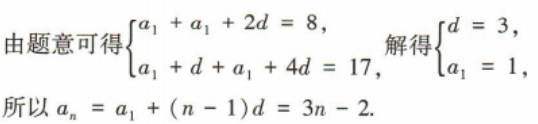2024年高职单招《数学(中职)》每日一练试题12月12日

2024年高职单招《数学(中职)》每日一练试题12月12日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、已知双曲线的焦距为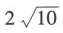,且双曲线的一条渐近线与直线3x+y=0垂直，则双曲线的方程为()  

• A：
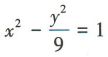
• B：
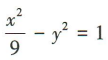
• C：
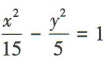
• D：

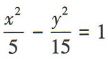
答 案：B

解 析：由双曲线的焦距为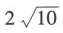得半焦距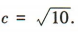因为双曲线的一条渐近线与直线3x+y=0垂直，且直线3x+y=0的斜率为-3,所以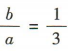,即a=3b.又a²+b²=c²,所以10b²=10,即b²=1,则a²=9,所以双曲线的方程为.

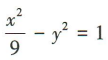2、函数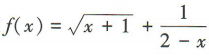的定义域为（）  

• A：[-1,2）U(2,+∞)
• B：[2,+∞）
• C：[-1,2)
• D：[-1,+∞)

答 案：A

解 析：要使函数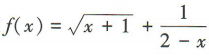，须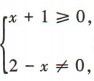有意义解得x≥-1且x≠2,故f(x)的定义域为[-1,2)U(2,+∞)。

3、过A(3,0),B(0,2)两点的直线的方程为（）  

• A：2x-3y-6=0
• B：3x+2y-4=0
• C：2x+3y-6=0
• D：x+2y-4=0

答 案：C

解 析：因为直线经过点 A(3,0)和 B(0,2),所以直线的方程为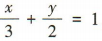，即2x+3y-6=0.

4、以点(-3,1)为圆心，且与直线3x+4y=0相切的圆的方程是（）  

• A：(x-3)²+(y+1)²=4
• B：(x+3)²+(y-1)²=4
• C：(x-3)²+(y+1)²=1
• D：(x+3)²+(y-1)²=1

答 案：D

解 析：易得圆心(-3,1)到直线3x+4y=0的距离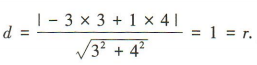又点(-3,1)为圆心，所以圆的方程为(x+3)²+(y-1)²=1.

填空题

1、函数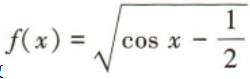的定义域为（）

答 案：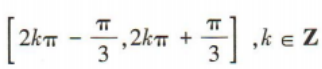

解 析：

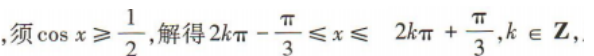
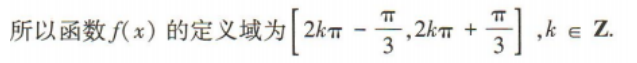
2、如图，画一个边长为4的正方形，再将这个正方形各边的中点相连得到第2个正方形，依此类推，这样一共画了10个正方形，则第10个正方形的面积为（）

答 案：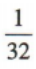

解 析：由题意知，第一个正方形的边长a1=4,面积T1=16;第二个正方形的边长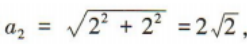面积T2=8;第三个正方形的边长a3=2,面积T3=4;第四个正方形的边长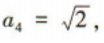面积T4=2,……,由此可发现规律，第n个正方形的面积

3、若向量a与b共线，且|a|=|b|=1,则|a+b|=（）  

答 案：0或2

解 析：∵向量a与b共线，且|a|=|b|,∴a与b相等或互为相反向量.当a与b相等时，|a+b|=|2a|=2;当a与b互为相反向量时，|a+b|=|0|=0.

4、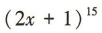的展开式中,含x⁵的项是第()项.  

答 案：11

解 析：易得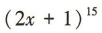的展开式的通项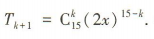令15-k=5,解得k=10,则含x⁵的项是展开式中的第 11 项.

简答题

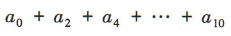1、已知,求的值.  

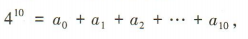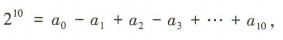答 案：令x=2得 令x=0得 所以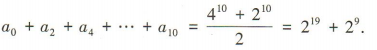  

2、设{a_n}是等差数列，已知a₁+a₃=8,a₂+a₅=17. (1)求{a_n}的通项公式 (2)求数列{a_n}的前n项和S_n.

答 案：