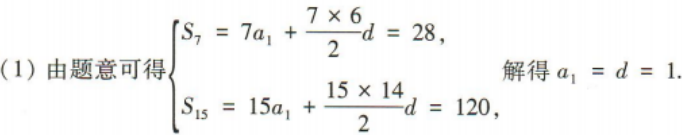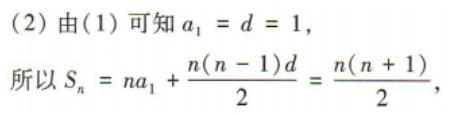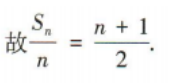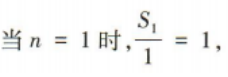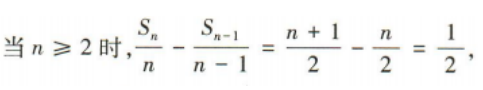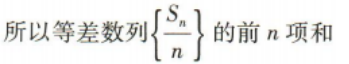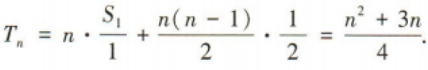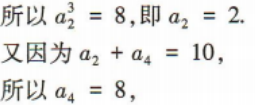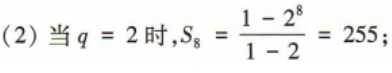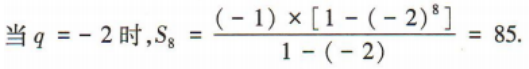2024年高职单招《数学(中职)》每日一练试题12月27日
2024-12-27 15:46:46 来源：人人学历网
2024年高职单招《数学(中职)》每日一练试题12月27日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。
单选题
1、不等式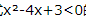
的解集为()
- A：
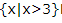
- B：
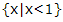
- C：
- D：
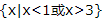
答 案：C
解 析：由方程x2-4x+3=0得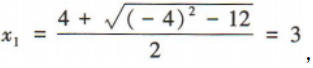
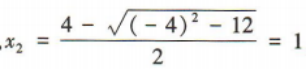,所以不等式x²-4x+3<0的解集为(1,3).
2、不等式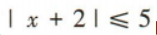
的解集是（）
- A：
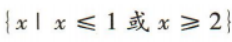
- B：
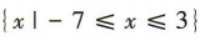
- C：
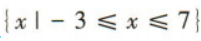
- D：
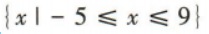
答 案：B
解 析：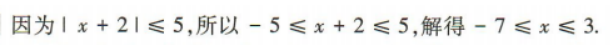
3、若函数f(x)在R上单调递增，且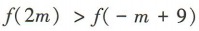
,则实数m的取值范围是()
- A：(1,+∞)
- B：(0,+∞)
- C：(3,+∞)
- D：(-∞,-3)U(3,+∞)
答 案：C
解 析：∵函数f(x)在R上单调递增，且,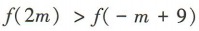
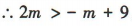,解得
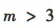,∴实数m的取值范围是(3,+∞).
4、
- A：充分不必要条件
- B：必要不充分条件
- C：充要条件
- D：既不充分也不必要条件
答 案：B
解 析：
填空题
1、已知平面向量a=(-3,m),b=(m-2,-1),若a与b的方向相反，则实数m的值为（）
答 案：3
解 析：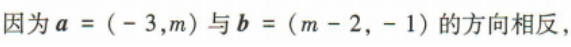
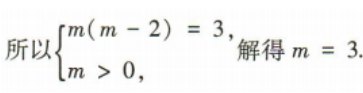
2、已知椭圆的标准方程为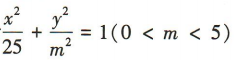
,且焦距为6,则实数 m 的值为()
答 案：4
解 析：由题意得 3、若 答 案： 解 析： 4、某医疗机构有4名新冠疫情防控志愿者,现要从这4人中选3个人去3个不同的社区进行志愿服务则不同的安排方法共有（）种.
答 案：24 解 析：由题意可分两步,第一步,从4名新冠疫情防控志愿者中选出3人,共有 简答题 1、已知等差数列{an}的前n项和为Sn且S7=28,S15=120 (1)求数列{an}的首项a1和公差d; (2)证明数列 答 案： 2、在等比数列{an}中，a1a2a3=8,a2+a4=10. (1)求首项a1及公比q; (2)求该数列的前8项和S8 答 案：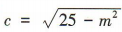
,所以
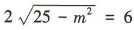,因为0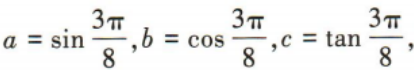
则a,b,c从小到大的顺序为（）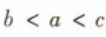
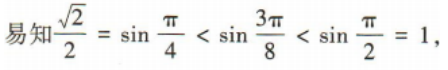
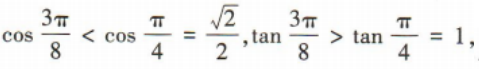
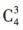种方法:第二步,选出的3人去3 个不同的社区,共有
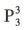种方法,根据分步乘法计数原理可知不同的安排方法共有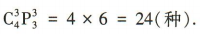
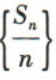是等差数列，并求出
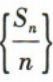的前n项和Tn
- 备考交流
-
单招真题交流3群
扫一扫或点击二维码入群
