2025年高职单招《数学(中职)》每日一练试题01月04日

2025年高职单招《数学(中职)》每日一练试题01月04日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

单选题

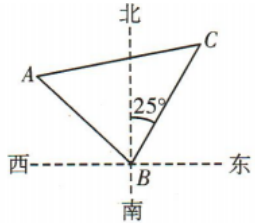
1、一艘船航行到点A处时，测得灯塔C与点A相距30海里，如图所示.随后该船以20海里/时的速度，沿直线向东南方向航行1小时后到达点B,测得灯塔C在点B的北偏东25°方向，则sin∠ACB=（）

• A：
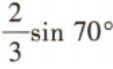
• B：
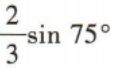
• C：
• D：

答 案：A

解 析：由题意可知，∠ABC=45°+25°=70°,AB=20,AC=30.在△ABC中，由正弦定理可得

2、不等式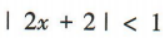的解集为（）

• A：
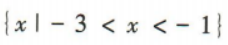
• B：
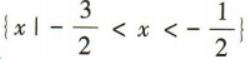
• C：
• D：

答 案：B

解 析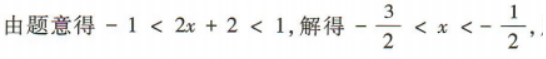： 所以选B

3、抛物线x²=8y的准线方程为()  

• A：x=-2
• B：y=-2
• C：x=2
• D：y=2

答 案：B

解 析：易知抛物线x²=8y的焦点在y轴正半轴上，且2p=8,即p=4,所以抛物线x²=8y的准线方程为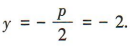

4、若椭圆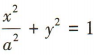的一个焦点坐标为(2,0),则此椭圆的方程为()  

• A：
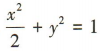
• B：
• C：
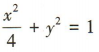
• D：

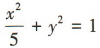
答 案：D

解 析：因为椭圆的标准方程为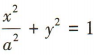,一个焦点坐标为(2,0),所以c=2,b=1,所以a²=b²+c²=5,所以椭圆的方程为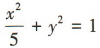

填空题

1、某公司4,B,C三种不同型号产品的库存数量之比为2:3:1,为检验产品的质量,现采用分层抽样的方法从库存产品中抽取一个样本,若在抽取的产品中,恰有A型号产品18 件,则该样本容量是()  

答 案：54

解 析：设样本容量是n,由题意得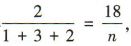解得 n= 54.

2、在等比数列{an}中，a₁=1,a₂=3,则a₅=（）

答 案：81

解 析：

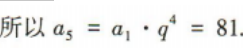
3、斜率为2的直线经过 A(3,5),B(a,7)两点,则a的值为（）  

答 案：4

解 析：由题意得直线 AB 的斜率 k_AB= 2,即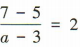,解得a= 4.

4、等比数列{a_n}中,a₁=1,a₂a₅=8a₁a₃,则a₃=（）

答 案：4

解 析：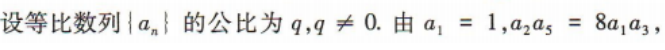

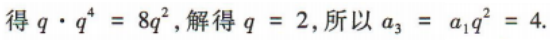
简答题

1、如图,已知 A,B,C,D是空间中四点,且点A,B,C在同一直线l上,点D不在直线l上,证明直线 AD,BD,CD在同一平面内.  

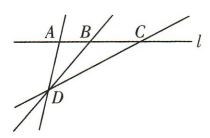
答 案：因为点A,B,C在同一直线l上,点D不在直线l上,过直线与直线外一点有且只有一个平面， 所以点 A,B,C,D确定唯一的一个平面,设为α, 所以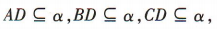 所以直线 AD,BD,CD 在同一平面内.

2、已知圆C过点A(6,0),B(1,5),且圆心在直线l:2x-7y+8=0上.(1)求圆C的标准方程;
(2)求过B点,且与圆C相切的直线方程.  

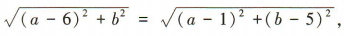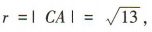答 案：(1)设圆心C的坐标为(a,b). 因为圆C过点A(6,0),B(1,5), 所以|CA|=|CB|,即 所以a-b-1=0. 又圆心在直线l:2x-7y+8=0上， 所以2a-7b+8=0, 所以a=3,b=2, 所以圆心为C(3,2),半径 所以圆C的标准方程是(x-3)²+(y-2)²= 13. (2)由(1)知 C(3,2),直线 BC 的斜率为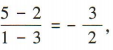 所以所求切线的斜率为 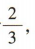故所求切线的方程为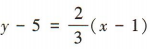,即2x-3y+13 =0.