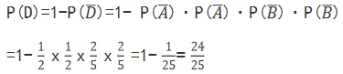2025年高职单招《数学(中职)》每日一练试题01月14日

2025年高职单招《数学(中职)》每日一练试题01月14日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、若角的顶点在原点，始边与x轴的非负半轴重合，则与2023°角终边相同的最小正角为()  

• A：23°
• B：137°
• C：223°
• D：337°

答 案：C

解 析：因为2023°=360°×5+223°,所以与2023°角终边相同的最小正角为223°.

2、若指数函数y=(a+1)^x是增函数，则a的取值范围是（）

• A：(-1,0]
• B：(-1,0)
• C：(0,+∞)
• D：[0,+∞)

答 案：C

解 析：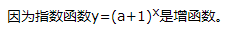

3、已知向量a,b满足|a|=5，|b|=6，a·b=-6，则cos=（）  

• A：
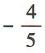
• B：
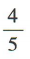
• C：
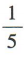
• D：

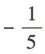
答 案：D

解 析：因为|a|=5,|b|=6,a·b=-6,所以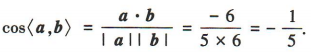

主观题

1、已知

答 案：方法一：矢量图表示法 矢量图表示法如图所示。 方法二：矢量表示法

解 析：

填空题

1、将2.5.11三个数分别加上相同的常数m.使得到的三个数依次成等比数列，则m=（）  

答 案：1

解 析：2+m,5+m,11+m三个数依次成等比数列，所以(5+m)²=(2+m)(11+m),解得m=1.    

2、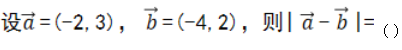  

答 案：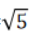

解 析：

3、若向量a与b共线，且|a|=|b|=1,则|a+b|=（）  

答 案：0或2

解 析：∵向量a与b共线，且|a|=|b|,∴a与b相等或互为相反向量.当a与b相等时，|a+b|=|2a|=2;当a与b互为相反向量时，|a+b|=|0|=0.

简答题

1、甲、乙两人进行投篮训练，己知甲投球命中的概率是1/2，乙投球命中的概率是3/5,且两人投球命中与否相互之间没有影响. (1) 若两人各投球1次，求恰有1人命中的概率; (2) 若两人各投球2次，求这4次投球中至少有1次命中的概率

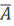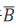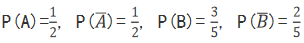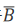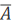答 案：解:记甲投球命中为事件A，甲投球未命中为事件:乙投球命中为事件B，乙投球未命中为事件 则 (1)记两人各投球1次，恰有1人命中为事件C,则P(C)= P(A)·P()+ P()·P(B) =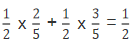 (2)记两人各投球2次，4次投球中至少有1次命中为事件D,则.两人各投球2次，4次投球中全未命中为事件