2025年高职单招《数学》每日一练试题05月12日

2025年高职单招《数学》每日一练试题05月12日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过高职单招每日一练的积累，助力我们更容易取得最后的成功。

判断题

1、函数f（x）=（x-1）（x²+3x-10）有3个零点。（）  

答 案：对

2、当x∈R时，函数y=2sinx+1的值域为[-1,3]。（）  

答 案：对

解 析：当x∈R时，函数sinx值域为[-1，1]，2sinx值域为[-2，2]，函数y=2sinx+1的值域为[-1，3]，故正确。

单选题

1、下列长度中的各组线段中，是勾股数的一组是()  

• A：0.3，0.4，0.5
• B：4，5，6
• C：9，10，12
• D：30，40，50

答 案：D

解 析：勾股数的定义就要求所有的数必须为"正整数"

2、sin30°=（）  

• A：
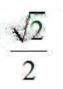
• B：1/2
• C：
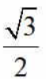
• D：

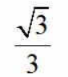
答 案：B

解 析：根据特殊角的三角函数值进行解答即可

多选题

1、已知等差数列{a_n}的前n项和为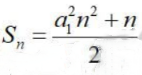，公差为d，则（）  

• A：a₁=1
• B：d=1
• C：
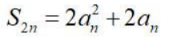
• D：2S_n-a_n=1+3+5+...+(2n-1)

答 案：ABD

2、下列计算结果正确的是（）  

• A：
• B：
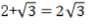
• C：
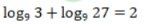
• D：

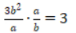
答 案：AC

主观题

1、已知抛物线C:x²=4y和直线7:2x+2y+m=0. (1)若抛物线C和直线l有两个交点，求m的取值范围； (2)若m＞1,且直线l与抛物线C有两个交点A,B,线段AB的垂直平分线交y轴于点P,求△PAB的面积S的取值范围。  

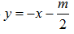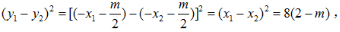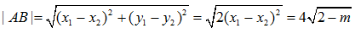答 案：（1）由2x+2y+m=0得 将其代入x²=4y中得x²+4x+2m=0， 所以△=4²-4×1×2m=16-8m. 因为抛物线C和直线l有两个交点，所以△=16-8m＞0，解得m＜2. 因此，m的取值范围是（-∞，2） （2）设点A（x₁，,y₁），B（x₂，y₂），则由方程x²+4x+2m=0可得x₁+x₂=-4，x₁x₂=2m， （x₁-x₂)²=（x₁+x₂)²-4x₁x₂=8（2-m）; 所以 因为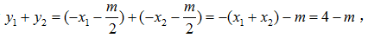 所以线段AB的中点 k_AB=-1， 所以过点Q与线段AB垂直的直线方程为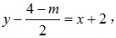 即2x-2y+8-m=0. 该直线与y轴的交点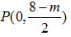到直线l的距离 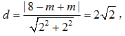所以△PAB的面积 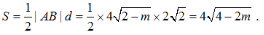因为1＜m＜2，所以0＜4-2m＜2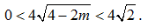， 因此，△PAB的面积S的取值范围是（0，4√2）  

2、甲、乙两支球队进行比赛，约定先胜3局者获得比赛的胜利，比赛随即结束.除第五局甲队获胜的概率是外，其余每局比赛甲队获胜的概率都是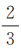.假设各局比赛结果相互独立. (1)分别求甲队以3:0,3:1,3:2获得比赛胜利的概率； (2)若比赛结果为3:0或3:1,则胜利方得3分，对方得0分；若比赛结果为3:2,则胜利方得2分，对方得1分.求乙队得分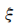的分布列和数学期望.  

答 案：（1）设“甲队以3:0胜利”为事件A，“甲队以3:1胜利”为事件B，“甲队以3:2胜利”为事件C，则 （2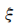）的所有可能取值为0,1,2,3,设“乙队以3:2胜利”为事件D，由于各局比赛结果相互独立， 则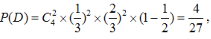 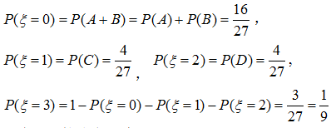因此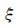，的分布列为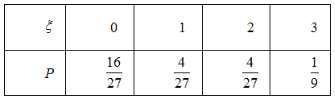 的数学期望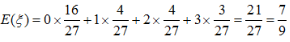  

填空题

1、经过点M(-2,m),N(m,4)的直线的斜率等于1,则m的值为（）  

答 案：

解 析：由题意可知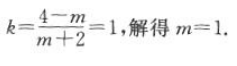  

2、若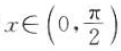,则函数y=sin x+cos x的值域为（）.

答 案：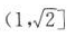

解 析：因为函数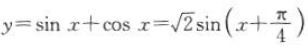,所以时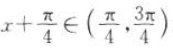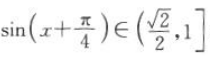，,,函数y=sin x+cos x的值域为