首页 课程学习 题库 APP下载 院校查询
注册 帮助中心 合作联系
当前位置：首页 > 考试 > 学历类 > 成考高起点 > 数学(理) >
2025年成考高起点每日一练《数学(理)》2月1日

2025年成考高起点每日一练《数学(理)》2月1日

考试总分：10分

考试类型：模拟试题

作答时间：60分钟

已答人数：1137

试卷答案：有

试卷介绍： 2025年成考高起点每日一练《数学(理)》2月1日专为备考2025年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

开始答题

试卷预览

单选题 主观题 填空题
  • 1. 已知集合M =(2,3,5,a),N =(1,3,4,b),若M∩N=(1,2,3),则a,b的值为  

    Aa=2,b=1

    Ba=1,b=1

    Ca=1,b= 2

    Da=1,b=5

  • 2. 设全集U={0，1，2，3，4}，集合M={0，1，2，3，}，N={2，3，4}，则CuM∩CuN=（）。

    A{2，3）

    B{0，1，4}

    Cφ

    DU

  • 3. 设F1和F2为双曲线的两焦点,点P在双曲线上,则||PF2|-|PF2||=（）。

    A4

    B2

    C1

    D

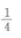
  • 4. 已知棱长为1的正方体ABCD-A’B’C’D’（）。

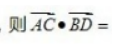    A

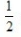
    B0

    C

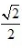
    D

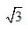
  • 1. 已知等差数列前n项和 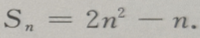（Ⅰ）求这个数列的通项公式;（Ⅱ）求数列第六项到第十项的和
  • 2. 设分别讨论x→0及x→1时f（x）的极限是否存在？
  • 3. 求（1+tan10°）（1+tan35°）的值。  
  • 4. 在正四棱柱ABCD-A'B'C'D'中， （Ⅰ）写出向量关于基底{a,b,c}的分解式 （Ⅱ）求证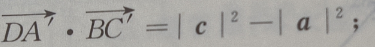： （Ⅲ）求证：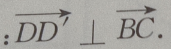  
  • 1. 已知A（0,1），B（1，2），存在一点P是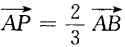，则点P的坐标是______。
  • 2. 化简sin（x+y）-2cosxsiny=______.  
相关试卷
相关题库