首页 课程学习 题库 APP下载 院校查询
注册 帮助中心 合作联系
当前位置：首页 > 考试 > 学历类 > 高职单招 > 数学 >
2025年高职单招每日一练《数学》2月22日

2025年高职单招每日一练《数学》2月22日

考试总分：10分

考试类型：模拟试题

作答时间：60分钟

已答人数：1800

试卷答案：有

试卷介绍： 2025年高职单招每日一练《数学》2月22日专为备考2025年数学考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

开始答题

试卷预览

判断题 单选题 多选题 主观题 填空题
  • 1. y=3tanx的最小正周期为3π。（）  

    A对

    B错

  • 2. 三点确定一个平面。（）  

    A对

    B错

  • 1. 用配方法解方程x2-8x+2=0，则方程可变形为（）  

    A（x-4）2=5

    B（x+4）2=21

    C（x-4）2=14

    D（x-4）2=18

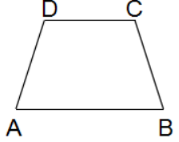
  • 2. 如图，等腰梯形ABCD中，AB//DC，AD=BC=8，AB=10，CD=6，则梯形ABCD的面积是（）  

    A

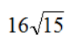
    B

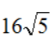
    C

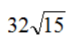
    D

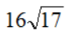
  • 1. 已知等差数列{an}的前n项和为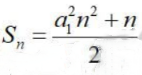，公差为d，则（）  

    Aa1=1

    Bd=1

    C

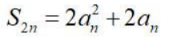
    D2Sn-an=1+3+5+...+(2n-1)

  • 2. 已知等差数列{an}的前n项和为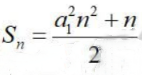，公差为d，则（）  

    Aa1=1

    Bd=1

    C2Sn-an=1+3+5+...+(2n-1)

    D

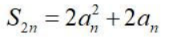
  • 1. 已知等差数列{an}的前n项和Sn且S5=35,S8=104.
    (1)求数列{an}的通项公式；
    (2)若{bn}为等比数列，b1=a2,b2=a3+2,求数列{b,}的公比q及前n项和Tn.
  • 2. 已知两直线,当m为何值时，l1与l2: (1)相交；(2)平行；(3)重合.  
  • 1. 盒中有3个白球和5个红球，任意取出一个球，取出的是红球的概率为_______  
  • 2. 若指数函数的图像经过点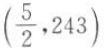,则其解析式为().
相关试卷
相关题库