首页 课程学习 题库 APP下载 院校查询
注册 帮助中心 合作联系
当前位置：首页 > 考试 > 学历类 > 成考高起点 > 数学(文史) >
2025年成考高起点每日一练《数学(文史)》4月23日

2025年成考高起点每日一练《数学(文史)》4月23日

考试总分：10分

考试类型：模拟试题

作答时间：60分钟

已答人数：454

试卷答案：有

试卷介绍： 2025年成考高起点每日一练《数学(文史)》4月23日专为备考2025年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

开始答题

试卷预览

单选题 主观题 填空题
  • 1. 下列各等式不成立的是（）。

    A3x·2x=6x

    B9x=（3x）2

    C

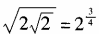
    D

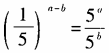
  • 2. 与圆x2+y2=4关于点M（3,2）成中心对称的曲线方程是（）

    A（x-3）2+（y-2）2=0

    B（x+3）2+（y+2）2=0

    C（x-6）2+（y-4）2=0

    D（x+6）2+（y+4）2=0

  • 3. A、B是抛物线y2=8x上两点，且此抛物线的焦点在线段AB上，已知A、B两点的横坐标之和为10，则|AB|=（）。

    A18

    B14

    C12

    D10

  • 4. 书架上层有6本不同的数学书，下层有4本不同的语文书，从中任取一本书，则不同的选法有（）。

    A10

    B6

    C4

    D24

  • 1. 已知等差数列{an}中，a1+a3+a5=6，a2+a4+a6=12，求{an}的首项与公差.  
  • 2. 在△ABC中，已知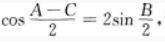证明a，b，c成等差数列。
  • 3. 已知log53=a，log54=b，求log2512关于a，b的表达式。  
  • 4. 已知函数f（x）=（x-4）（x2-a）。（I）求f’（x）；
    （Ⅱ）若f’（-1）=8，求f（x）在区间[0，4]的最大值与最小值。
  • 1. 一个问题在1小时内，甲能独立解决的概率是0.5，乙能独立解决的概率是0.4，两人在1小时内解决问题的概率是______。
  • 2. 为了考察某种小麦的长势，从中抽取10株苗，测得苗高如下(单位：cm)：12,13，14，15，10，16，13，11，15，11． 则该品种的小麦苗高的样本方差为__________cm2．
相关试卷
相关题库