2025年成考高起点《数学(理)》每日一练试题04月23日

2025年成考高起点《数学(理)》每日一练试题04月23日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、对满足a>b的任意两个非零实数，下列不等式成立的是（）  

• A：
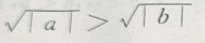
• B：
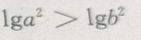
• C：
• D：

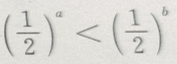
答 案：D

解 析：A错误，例如-2>4,而 B错误，例如：-10>100,而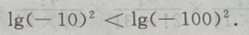 C错误，例如：-1>-2,而

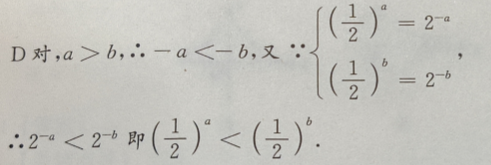
2、二项式(2x－1)⁶的展开式中，含x⁴项系数是（）。

• A：-15
• B：-240
• C：15
• D：240

答 案：D

解 析：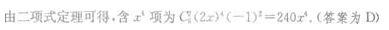

3、下列各等式不成立的是（）。

• A：3^x·2^x=6^x
• B：9^x=（3^x）2
• C：
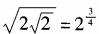
• D：

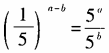
答 案：D

解 析：3^x·2^x=（3·2）^x=6^x，排除A；（3^x）²=（3²）^x=9^x，排除B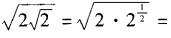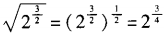；，排除C。选D。  

4、设集合M={1,2,4}，N={2,3,5}，则集合M∪N=（）.

• A：{2}
• B：{1，2，3，4，5}
• C：{3，5}
• D：{1，4}

答 案：B

解 析：M∪N={1,2,4}∪{2,3,5)= {1，2，3，4，5} (答案为B)

主观题

1、在△ABC中，B=120°,BC=4,△ABC的面积为，求AC.

答 案：由△ABC的面积为得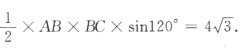所以AB =4.因此所以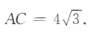

2、试证明下列各题
（1）
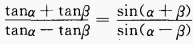
（2）

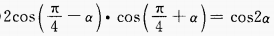
答 案：（1）化正切为正、余弦，通分即可得证。 （2）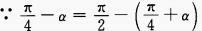

3、（1）已知tanα=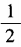，求cot2α的值； （2）已知tan2α=1，求tanα的值。

答 案：（1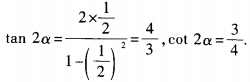）（2）由已知，得 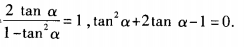解关于tanα的一元二次方程，得tanα=  

4、已知数列的前n项和 求证：是等差数列，并求公差和首项。  

答 案：  

填空题

1、已知≤0＜2π，且实数x满足log₃x=2-cos²θ+sin²θ，则x的最小值是______。  

答 案：3

解 析：因为log₃x=2-（cos²θ-sin²θ）=2-cos2θ。 又log₃x中的底数3＞1，因此要使x最小，应使2-cos2θ的值最小，而其最小值为1，故x=3。

2、一个问题在1小时内，甲能独立解决的概率是0.5，乙能独立解决的概率是0.4，两人在1小时内解决问题的概率是______。  

答 案：0.7

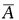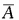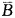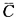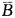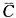解 析：设事件A为两人在1小时内解决问题，即1小时内至少有一人能解决问题，事件B为甲在1小时内解决问题，事件C为乙在1小时内解决问题，事件B、C是相互独立事件，事件A的对立事件 互为在1小时内两个人都没有解决问题，所以 P（A）=1-P（）=1-P（·）=1-P（）·P（） =1-（1-0.5）×（1-0.4）=1-（0.5×0.6）=1-0.3=0.7