2025年成考高起点《数学(文史)》每日一练试题02月08日
2025-02-08 12:24:11 来源:人人学历网
2025年成考高起点《数学(文史)》每日一练试题02月08日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、函数f(x)=x3-6x2+9x-3的单调区间为()。
- A:(-∞,-3),(-3,1),(1,+∞)
- B:(-∞,-1),(-1,3),(3,+∞)
- C:(-∞,-3),(-3,-1),(-1,+∞)
- D:(-∞,1),(1,3),(3,+∞)
答 案:D
解 析:∵x∈R
f’(x)=3x2-12x+9
=3(x2-4x+3)
=3(x-3)(x-1)
∴x>3或x<1,f’(x)>0,
1 2、已知一个等差数列的第五项等于10,前三项的和等于3,那么这个等差数列的公差为()。 答 案:A 3、已知两数的等差中项为10,等比中项为8,则以这两数为根的一元二次方程是()。 答 案:D 4、设集合M={x||x-2||<2},N={0,1,2,3,4},则M∩N=() 答 案:C 解 析:解得M={x||x-2||<2}={x|-2<x-2<2}={x|0<x<4},故M∩N={1,2,3}. 主观题 1、已知F是椭圆 答 案:(Ⅰ)由椭圆方程可知,椭圆的长半轴a=5,短半轴,则椭圆的半焦距 2、已知抛物线C:y2=2px(p>0)的焦点到准线的距离为1。(I)求C的方程; 答 案:(I)由题意,该抛物线的焦点到准线的距离为 3、已知log53=a,log54=b,求log2512关于a,b的表达式。
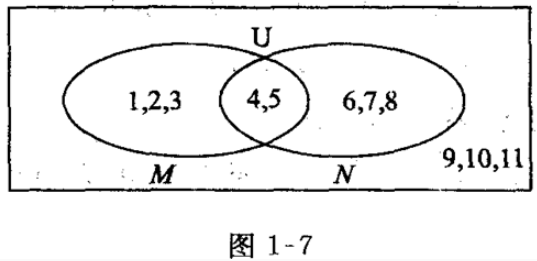
答 案: 4、已知等差数列 答 案:(Ⅰ)当n=1时,由 填空题 1、全集U,集合M,N如图1—7所示,用列举法表示M,N,CUM,CUN。 答 案:如图1—7,有M={1,2,3,4,5},N={4,5,6,7,8},CUM={6,7,8,9,10,11},CUN={1,2,3,9,10,11}。 2、袋中装有3个白球,2个红球,从中任取2个球,取到2个都是红球的概率是______。
答 案: 解 析: 的右焦点,点M在抛物线y2=2px(p>0)上O为坐标原点,且△MOF为正三角形.
(Ⅰ)求P的值; (Ⅱ)求抛物线的焦点坐标和准线方程.
的右焦点,点M在抛物线y2=2px(p>0)上O为坐标原点,且△MOF为正三角形.
(Ⅰ)求P的值; (Ⅱ)求抛物线的焦点坐标和准线方程. 即椭圆的右焦点F的坐标为
(4.0).
即椭圆的右焦点F的坐标为
(4.0). 如图,因为△MOF为正三角形,OF=4,过M作MN⊥OF于N点,
如图,因为△MOF为正三角形,OF=4,过M作MN⊥OF于N点, 【考点指要】本题主要考查椭圆、抛物线的概念,要求考生掌握它们的标准方程和性质,会用它们解决有关的问题.
【考点指要】本题主要考查椭圆、抛物线的概念,要求考生掌握它们的标准方程和性质,会用它们解决有关的问题.
(Ⅱ)若A(1,m)(m>0)为C上一点,O为坐标原点,求C上另一点B的坐标,使得OA⊥OB。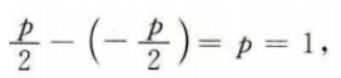 所以抛物线C的方程为y2=2x.
(Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得 m=
所以抛物线C的方程为y2=2x.
(Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得 m=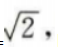 因此A点坐标为
因此A点坐标为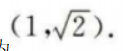 设B点坐标为
设B点坐标为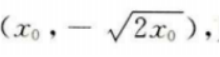
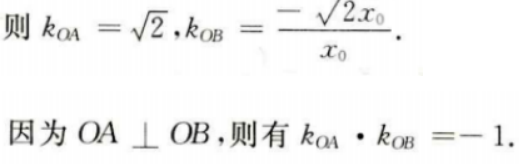


 前n项和
前n项和 (Ⅰ)求通项
(Ⅰ)求通项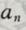 的表达式
(Ⅱ)求
的表达式
(Ⅱ)求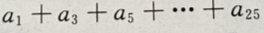 的值
的值
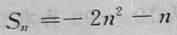 得
得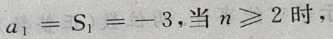
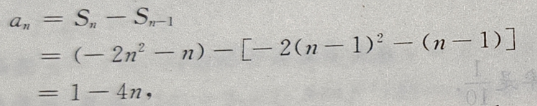
 也满足上式,故
也满足上式,故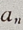 =1-4n(n≥1)
(Ⅱ)由于数列
=1-4n(n≥1)
(Ⅱ)由于数列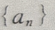 是首项为
是首项为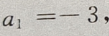 公差为d=-4的等差数列,所以
公差为d=-4的等差数列,所以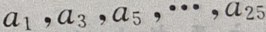 是首项为
是首项为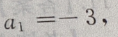 公差为d=-8,项数为13的等差数列,于是由等差数列前n项和公式得:
公差为d=-8,项数为13的等差数列,于是由等差数列前n项和公式得:

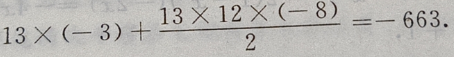

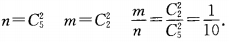
2025年成考高起点《数学(文史)》每日一练试题02月02日 02-02 2025年成考高起点《数学(文史)》每日一练试题01月02日 01-02 2025年成考高起点《数学(文史)》每日一练试题02月01日 02-01 2025年成考高起点《数学(文史)》每日一练试题02月03日 02-03 2025年成考高起点《数学(文史)》每日一练试题02月04日 02-04 2025年成考高起点《数学(文史)》每日一练试题01月08日 01-08 2023年成考高起点《数学(文史)》每日一练试题02月08日 02-08 2022年成考高起点《数学(文史)》每日一练试题08月02日 08-02



