2025年成考高起点《数学(理)》每日一练试题02月10日

2025年成考高起点《数学(理)》每日一练试题02月10日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、已知，则sin2α=（）

• A：
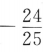
• B：
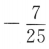
• C：
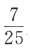
• D：

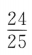
答 案：D

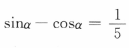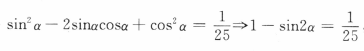解 析：两边平方得，故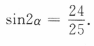

2、已知焦点在x轴上的椭圆的焦距等于2则该椭圆上任一点P到两焦点的距里之和为（）。

• A：8
• B：
• C：4
• D：

答 案：B

解 析：由题意可知a²=m,b²=4,2c=2,则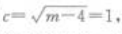,解得。a²=m-5,则该椭圆上任一点P到两焦点的距离之和为.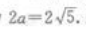(答案为B)

3、如果不共线的向量a和b有相等的长度,则(a+b)(a-b)=（）  

• A：0
• B：1
• C：-1
• D：2

答 案：A

解 析：(a+b)(a-b)=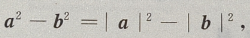

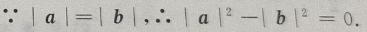
4、已知正方体ABCD-A'B’C’D'的棱长为1,则A’C与BC'所成角的余弦值为（）。

• A：
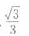
• B：
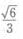
• C：
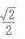
• D：

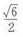
答 案：B

解 析：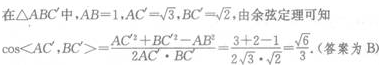

主观题

1、建筑一个容积为8000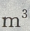,深为6m的长方体蓄水池，池壁每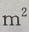的造价为15元，池底每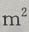的造价为30元。（I）把总造价y(元)表示为长x(m)的函数；（Ⅱ）求函数的定义域  

答 案：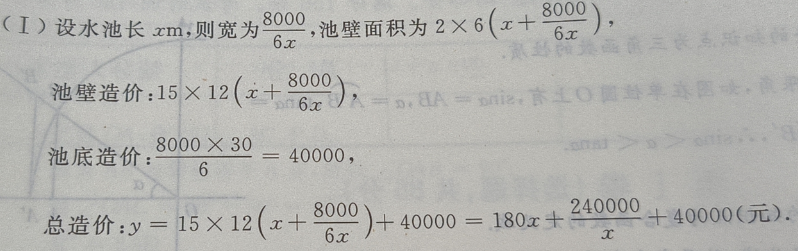

2、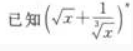 展开式的二项式系数之和比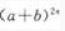展开式的二项式系数之和小240。 求：（1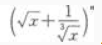）展开式的第3项；
（2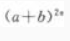）展开式的中间项。

答 案：

3、在△ABC中，B=120°,BC=4,△ABC的面积为，求AC.

答 案：由△ABC的面积为得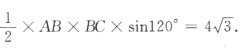所以AB =4.因此所以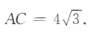

4、已知x+x^-1=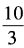，求x²+x-2的值。

答 案：由已知，得

填空题

1、已知≤0＜2π，且实数x满足log₃x=2-cos²θ+sin²θ，则x的最小值是______。  

答 案：3

解 析：因为log₃x=2-（cos²θ-sin²θ）=2-cos2θ。 又log₃x中的底数3＞1，因此要使x最小，应使2-cos2θ的值最小，而其最小值为1，故x=3。

2、lg(tan43°tan45°tan47°)=（）  

答 案：0

解 析：lg(tan43°tan45°tan47°)=lg(tan43°tan45°cot43°)=lgtan45°=lg1=0