2025年成考高起点《数学(文史)》每日一练试题03月07日

2025年成考高起点《数学(文史)》每日一练试题03月07日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、

• A：(-∞，-6)∪(1，+∞)
• B：(-6，1)
• C：(-∞，2)∪(3，+∞)
• D：(2，3)

答 案：B

解 析： 求必须有6-5x-x2>0，即x2+5x-6<0，即(x+6)(x-1)<0，解得-6，用区间表示为(-6，1)．此处应注意分母不能为零． 【考点指要】本题要求按二次根式定义域来解一元二次不等式，求定义域是成人高考的常见题．

2、对于函数，有下列两个命题：①如果c=o，那么y=f(x）的图像经过坐标原点②如果a<0，那么y=f(x）的图像与x轴有公共点
则（）

• A：①②都为真命题
• B：①为真命题，②为假命题
• C：①为假命题，②为真命题
• D：①②都为假命题

答 案：B

解 析：若c=0，则函数f(x)=ax²+bx过坐标原点，故①为真命题；若a＜0，而，则函数f(x)=ax²+bx+c的图像开口向下，与x轴没有交点，故②为假命题。因此选B选项。

3、设f（x）=x³+4x²+11x+7，则f（x+1）=（）。

• A：x³+7x²+22x+23
• B：x³—7x²+22x+23
• C：x³+7x²-22x+23
• D：x³-7x²-22x+23

答 案：A

解 析：f(x+1) =(x+1)³ +4(x+1}²+11(x+1)+7 =x³+3x²+3x+1+4x²+8x+4+11x+11+7 =x³+7x²+22x+23 综上所述，答案:x³+7x²+22x+23

4、已知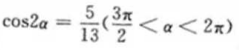,则tanα等于（）。

• A：2/3
• B：3/2
• C：-3/2
• D：-2/3

答 案：D

解 析：

主观题

1、若tanα、tanβ是关于x的方程mx²-(2m-3)x+m-2=0的两个实根，求tan(α+β)的取值范围

答 案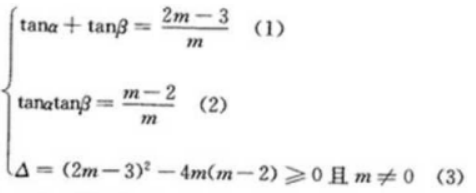： 由(1)(2)得，tan(a+β)=m-3/2;由(3)得m≤9/4且m≠0所以tan(a+β)的取值范围是(-∞，-3/2)U(-3/2，3/4)  

2、弹簧的身长与下面所挂砝码的重量成正比，知弹簧挂20g重的砝码时长度是12cm,挂35g重的砝码时长度是15cm，写出弹簧长度y(cm)与砝码重x(g)的函数关系式，并求弹簧不挂砝码时的长度

答 案：设弹簧原长为y0cm，则弹簧伸长量为（y-y0）cm， 由题意得y-y0=kx,即y=kx+y0, 由已知条件得 解得k=0.2，y0=8. 所求函数关系式为y=0.2x+8，弹的原长为8CM  

3、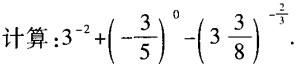  

答 案：

4、（1）已知tanα=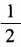 求cot2α的值； （2）已知tan2α=1，求tanα的值。

答 案：（1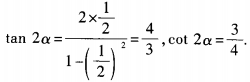） （2）由已知，得 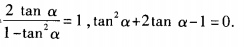解关于tanα的一元二次方程，得tanα=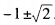

填空题

1、九个学生期末考试的成绩分别为79 63 88 94 99 77 89 81 85这九个学生成绩的中位数为______。  

答 案：85  

解 析：本题主要考查的知识点为中位数. 将成绩按由小到大排列：63，77，79，81，85，88，89，94，99.因此中位数为85。

2、已知tanθ=1/2，则sin2θ+sin2θ=__________．

答 案：1

解 析：