2025年成考高起点《数学(理)》每日一练试题03月23日
2025-03-23 12:12:38 来源:人人学历网
2025年成考高起点《数学(理)》每日一练试题03月23日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、下列函数中,为减函数的是()
- A:
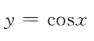
- B:
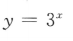
- C:
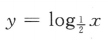
- D:
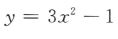
答 案:C
解 析:由对数函数的性质可知,当底数大于0小于1时,在定义域内,对数函数为减函数.
2、已知x+x-1=2cos40°,则x4+x-4=().
- A:2cos20
- B:-2cos20°
- C:2sin80°
- D:-2sin80°
答 案:B
解 析:由已知得(x+x-1)2=(2 cos 40°)2,x2+2+x-2=4cos240°,x2+x-2=2(2 cos240°-1)=2cos 80°同样可得x4+x-4=2 cos 160°=-2 cos 20°
3、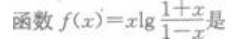 ()。
()。
- A:奇函数
- B:偶函数
- C:非奇非偶函数
- D:无法判断
答 案:B
解 析: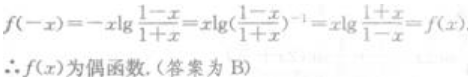
4、设log2x=a,则log2(2x2)=()。
- A:2a2+1
- B:2a2-1
- C:2a-1
- D:2a+1
答 案:D
解 析:本题主要考查的知识点为对数函数的性质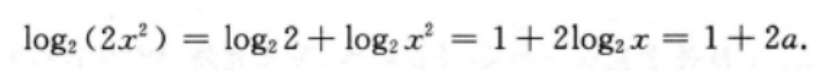
主观题
1、设函数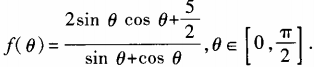 (1)求
(1)求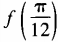 ;(2)求函数f(θ)最小值。
;(2)求函数f(θ)最小值。
答 案:
2、已知a,b,c成等差数列,a,b,c+1成等比数列.若b=6,求a和c.
答 案:由已知得 解得
解得
3、当自变量为何值时,函数y=2x3-3x2-12x+21有极值,其极值为多少?
答 案:y'=6x2-6x-12=6(x-2)(x+1) 当x<-1或x>2时,y>0,当-1
4、化简: (1)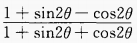
(2)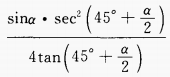
答 案:(1) (2)
(2)
填空题
1、函数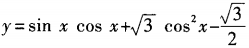 (x∈R)的最小值为______。
(x∈R)的最小值为______。
答 案:-1
解 析: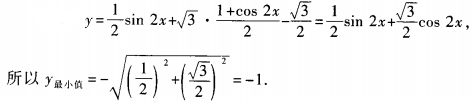
2、sin210°+sin220°+sin240°+sin250°+sin270°+sin280=______。
答 案:3
解 析:由互为余角的余函数值相等得 原式=(sin210°+cos210°)+(sin220°+cos220°)+(sin240+cos240)=1+1+1=3



