2024年成考专升本《高等数学一》每日一练试题11月28日
2024-11-28 11:29:54 来源:人人学历网
2024年成考专升本《高等数学一》每日一练试题11月28日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考专升本每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、 ()。
()。
- A:x=-2
- B:x=1
- C:x=2
- D:x=3
答 案:B
解 析:所给级数为不缺项情形, 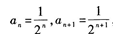

2、过点(1,0,0),(0,1,0),(0,0,1)的平面方程为()。
- A:x+y+z=1
- B:2x+y+z=1
- C:x+2y+z=1
- D:z+y+2z=1
答 案:A
解 析:方法一:设所求平面方程为Ax+By+Cz+D=0.由于点(1,0,0),(0,1,0),(0,0,1)在平面上,将上述三点坐标分别代入所设方程,可得A+D=0,B+D=0,C+D=0,即A=B=C=-D,再代回方程可得x+y+z=1。方法二:由于点(1,0,0),(0,1,0),(0,0,1)分别位于x轴、y轴、z轴上,可由平面的截距式方程得出x+y+z=1即为所求平面方程。
3、若f(x)为[a,b]上的连续函数,则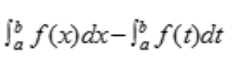 ()。
()。
- A:小于0
- B:大于0
- C:等于0
- D:不确定
答 案:C
解 析:f(x)为[a,b]上的连续函数,故 存在,它为一个确定的常数,由定积分与变量无关的性质,可知
存在,它为一个确定的常数,由定积分与变量无关的性质,可知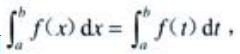 故
故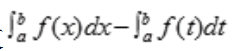 =0。
=0。
主观题
1、将函数f(x)=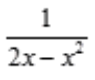 展开为x-1的幂级数,并指出收敛区间(不讨论端点)。
展开为x-1的幂级数,并指出收敛区间(不讨论端点)。
答 案:解: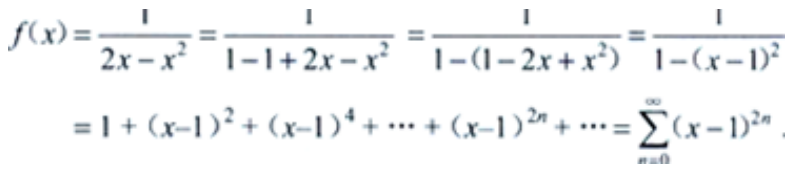 由
由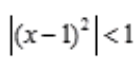 ,知-1<x-1<1,0<x<2,即收敛区间是(0,2)。
,知-1<x-1<1,0<x<2,即收敛区间是(0,2)。
2、设曲线x=√y、y=2及x=0所围成的平面图形为D.(1)求平面图形D的面积S。
(2)求平面图形D绕y轴旋转一周所生成旋转体的体积Vy。
答 案:解:D的图形见右图阴影部分。 (1)由
(1)由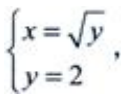 解得
解得 于是
于是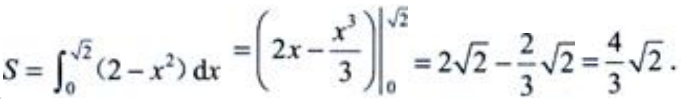
(2)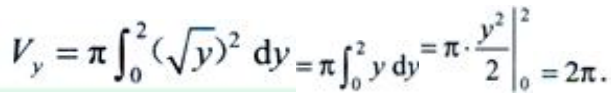
3、求函数y=xex的极小值点与极小值
答 案:解:方法一: 令y'=0,得x=-1。
令y'=0,得x=-1。
当x<-1时,y'<0;当x>-1时,y'>0。
故极小值点为x=-1,极小值为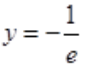 。
。
方法二:,
令y'=0,得x=-1,又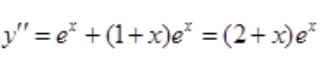 ,
, 。
。
故极小值点为x=-1,极小值为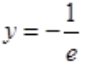 。
。
填空题
1、设f'(x0)=2,f(x0)=0,则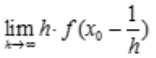 =()。
=()。
答 案:-2
解 析: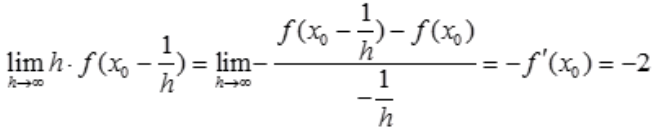 。
。
2、设函数z=xy,则全微分dz_______.
答 案: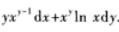
解 析: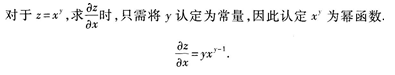

3、过原点且与平面2x-y+3z+5=0平行的平面方程为______。
答 案:2x-y+3z=0
解 析:已知平面的法线向量n1=(2,-1,3),所求平面与已知平面平行,因此可取所求平面的法线向量n=n1=(2,-1,3),又平面过原点(0,0,0),由平面的点法式方程可知,所求平面方程为2x-y+3z=0。
简答题
1、计算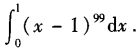
答 案: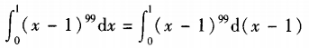
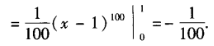
解 析:本题考查的知识点为定积分的计算。



