2025年成考专升本《高等数学一》每日一练试题06月11日
2025-06-11 11:33:48 来源:人人学历网
2025年成考专升本《高等数学一》每日一练试题06月11日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考专升本每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、当x→0时,下列函数以零为极限的是()。
- A:
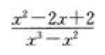
- B:
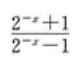
- C:
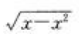
- D:

答 案:C
解 析:A项,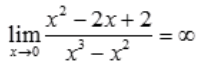 ;B项,
;B项,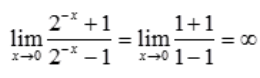 ;C项,
;C项,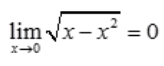 ;D项,
;D项,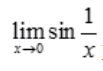 不存在。
不存在。
2、下列等式成立的是()
- A:
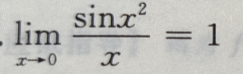
- B:
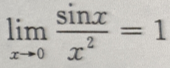
- C:
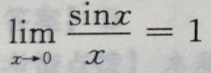
- D:
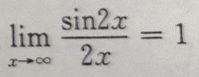
答 案:C
解 析:由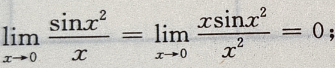
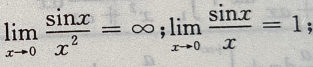
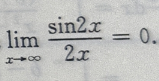
3、在空间直角坐标系中,方程x2+z2=z的图形是()。
- A:圆柱面
- B:圆
- C:抛物线
- D:旋转抛物面
答 案:A
解 析:方程x2+z2=z可变形为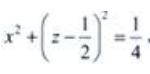 ,由此知该方程表示的是准线为圆、母线平行于y轴的圆柱面。
,由此知该方程表示的是准线为圆、母线平行于y轴的圆柱面。
主观题
1、计算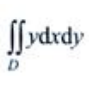 ,其中D为x2+y2=1,y=x及y=0和第一象限所围成的图形.
,其中D为x2+y2=1,y=x及y=0和第一象限所围成的图形.
答 案:解:在极坐标系中,D可表示为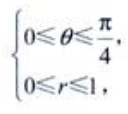 则
则
2、计算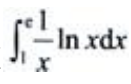 .
.
答 案:解:
3、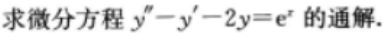
答 案:
填空题
1、过点M0(1,-1,0)且与平面x-y+3z=1平行的平面方程为=()。
答 案:x-y+3z=2
解 析:已知平面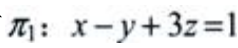 的法向量n1=(1,-1,3),所求平面π与π1平行,则平面π的法向量n//n1,取n=(1,-1,3),所求平面过点M0=(1,-1,0),由平面的点法式方程可知所求平面方程为
的法向量n1=(1,-1,3),所求平面π与π1平行,则平面π的法向量n//n1,取n=(1,-1,3),所求平面过点M0=(1,-1,0),由平面的点法式方程可知所求平面方程为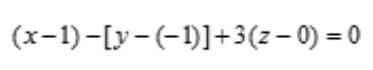 ,即x-y+3z=2。
,即x-y+3z=2。
2、曲线y=1-x-x3的拐点是()。
答 案:(0,1)
解 析:y=1-x-x3,则y'=-1-3x2,y''=-6x,令y''=0得x=0,y=1。当x<0时,y''>0;x>0时,y''<0.故曲线的拐点为(0,1)。
3、微分方程 的通解是()。
的通解是()。
答 案:y=-ex+Ce2x
解 析:该方程为一阶线性微分方程,通解为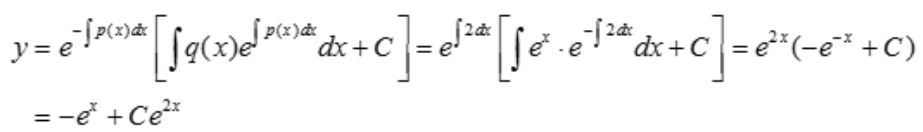
简答题
1、求由曲线y=3-x2与y=2x,y轴所围成的平面图形的面积及该封闭图形绕x轴旋转一周所成旋转体的体积。
答 案:所给曲线围成的平面图形如图1-2所示。 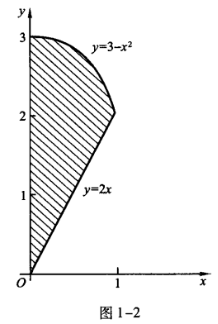 解法1利用定积分求平面图形的面积。
解法1利用定积分求平面图形的面积。

解 析:本题考查的知识点有两个:利用定积分求平面图形的面积;用定积分求绕坐标轴旋转所得旋转体的体积。



