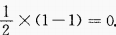2025年成考高起点《数学(理)》每日一练试题05月26日

2025年成考高起点《数学(理)》每日一练试题05月26日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、已知，则sin2α=（）

• A：
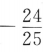
• B：
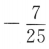
• C：
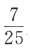
• D：

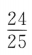
答 案：D

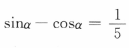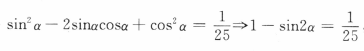解 析：两边平方得，故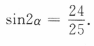

2、函数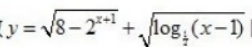的定义域为（）。

• A：{x|x>1}
• B：{x|x≤2}
• C：{x|1
• D：{x|1

答 案：D

3、对满足a>b的任意两个非零实数，下列不等式成立的是（）  

• A：
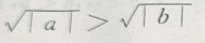
• B：
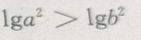
• C：
• D：

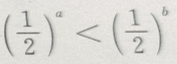
答 案：D

解 析：A错误，例如-2>4,而 B错误，例如：-10>100,而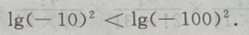 C错误，例如：-1>-2,而

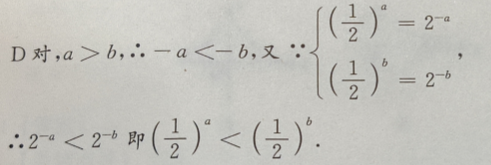
4、二次函数y＝2x²＋mx－5在区间(－∞，－1)内是减函数，在区间(－1，＋∞)内是增函数，则m的值是（）。

• A：4
• B：-4
• C：2
• D：-2

答 案：A

解 析：由题意可知二次函数y=2x²+mx-5的对称轴方程为x=-1,又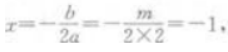解得m=4

主观题

1、已知设△ABC的三边长为a、b、C，2sin²A=3（sin²B+sin²C）且cos2A+3cosA+3cos（B-C）=1，求证：a：b：c=：1：1。

答 案：因所证的是△ABC三边的比，所以可将题中角的关系式转化为边的关系式，需用正弦定理关于题中的余弦关系式可通过恒等变形化为正弦函数的关系式。 ∵2sin²A=3（sin²B+sin²C）…① 由正弦定理得，2a²=3（b²+c²）…②
∵cos2A+3cosA+3cos（B-C）=1
∴3[cosA+cos（B-C）]=1-cos2A.
∵A=180°-（B+C）
∴3[-cos（B+C）+cos（B-C）]=2sin²A. 由两角和与差的余弦公式得
6sinBsinB=2sin²A…③
由①③得，2sinBsinC=sin²B+sin²C.
sin²B-2sinBsinC+sin²C=0
（sinB-sinC）²=0
sinB= sinC.
由正弦定理得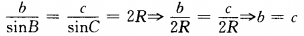

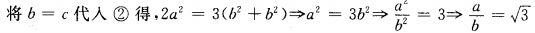
∴a：b=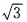：1
于是a：b：c=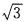：1：1。  

2、

答 案：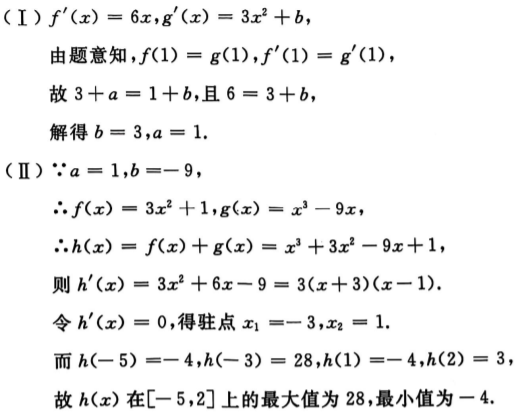

解 析：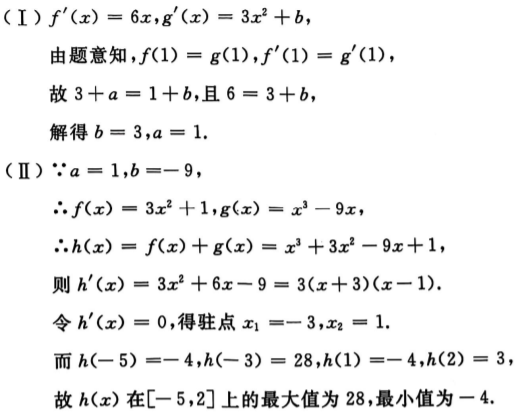

3、空间有四个点，如果其中任何三点不在同一直线上，可以确定几个平面?  

答 案：根据公理，在所给定的四点中任取三点，可确定一个平面，由组合公式所以共可确定四个平面。

解 析：空间有n个点，如果其中任何三点不在同一直线上，可以确定个平面。  

4、求下列函数的最大值、最小值和最小正周期： （1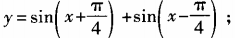）（2）y=6cosx+8sinx

答 案：  

填空题

1、九个学生期末考试的成绩分别为79 63 88 94 99 77 89 81 85这九个学生成绩的中位数为______。  

答 案：85  

解 析：本题主要考查的知识点为中位数. 将成绩按由小到大排列：63，77，79，81，85，88，89，94，99.因此中位数为85。

2、y=cos²2x的最大值是______，最小值______，周期T=______。  

答 案：1；0；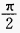

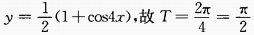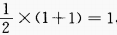解 析：，最大值为，最小值为