2025年成考高起点《数学(文史)》每日一练试题06月04日
2025-06-04 12:28:09 来源:人人学历网
2025年成考高起点《数学(文史)》每日一练试题06月04日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、在等比数列{an}中,a2=1,公比q=2,则a5=()。
- A:
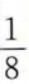
- B:
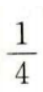
- C:4
- D:8
答 案:D
解 析:本题主要考查的知识点为等比数列。
2、下列函数中,为奇函数的是()。
- A:y=log3x
- B:y=3x
- C:y=3x2
- D:y=3sinx
答 案:D
3、圆C1:x2+y2=1与圆C2:x2+y2-4x=0的位置关系是()。
- A:外切
- B:内切
- C:相交
- D:相离
答 案:C
4、函数f(x)=x3-6x2+9x-3的单调区间为()。
- A:(-∞,-3),(-3,1),(1,+∞)
- B:(-∞,-1),(-1,3),(3,+∞)
- C:(-∞,-3),(-3,-1),(-1,+∞)
- D:(-∞,1),(1,3),(3,+∞)
答 案:D
解 析:∵x∈R
f’(x)=3x2-12x+9
=3(x2-4x+3)
=3(x-3)(x-1)
∴x>3或x<1,f’(x)>0,
1 主观题 1、(1)已知tanα= 答 案:(1) 2、已知等差数列{an}中,a1+a3+a5=6,a2+a4+a6=12,求{an}的首项与公差.
答 案:因为{an}为等差数列,则 3、设函数 答 案:(I)因为 4、设3a=5b=15,求a-1+b-1的值。
答 案:由3a=15,得a=log315;又由5b=15,得b=log515。 因此a-1+b-1= 解 析:过程中应用了换底公式的推论,即 填空题 1、从甲、乙、丙3名学生中随机选2人,则甲被选中的概率为 . 答 案: 解 析: 2、过点(2,0)作圆x2+y2=1的切线,切点的横坐标为()。 答 案: 解 析:本题主要考查的知识点为圆的切线.
设切点(x0,y0)则有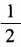 求cot2α的值; (2)已知tan2α=1,求tanα的值。
求cot2α的值; (2)已知tan2α=1,求tanα的值。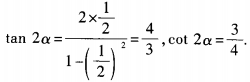 (2)由已知,得
(2)由已知,得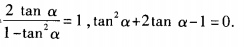 解关于tanα的一元二次方程,得tanα=
解关于tanα的一元二次方程,得tanα=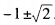

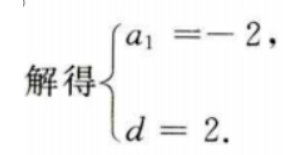
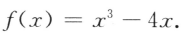
(I)求f'(2);
(II)求f(x)在区间[一1,2]的最大值与最小值.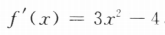 ,所以f'(2)=3×22-4=8.(II)因为x<-1,f(-1)=3.
,所以f'(2)=3×22-4=8.(II)因为x<-1,f(-1)=3.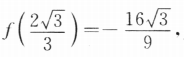 f(2)=0.
f(2)=0.
所以f(x)在区间[一1,2]的最大值为3,最小值为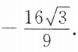
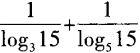 =log153+log155=1。
=log153+log155=1。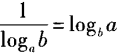
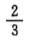
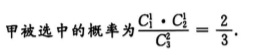
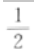
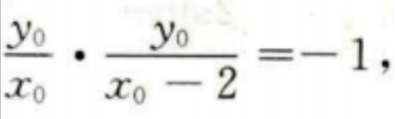 即
即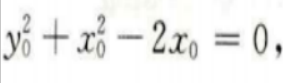
 所以
所以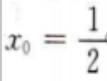 故切点横坐标为
故切点横坐标为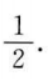
2025年成考高起点《数学(文史)》每日一练试题04月06日 04-06 2025年成考高起点《数学(文史)》每日一练试题04月04日 04-04 2024年成考高起点《数学(文史)》每日一练试题06月04日 06-04 2024年成考高起点《数学(文史)》每日一练试题04月06日 04-06 2023年成考高起点《数学(文史)》每日一练试题04月06日 04-06 2023年成考高起点《数学(文史)》每日一练试题06月04日 06-04 2025年成考高起点《数学(文史)》每日一练试题03月06日 03-06 2025年成考高起点《数学(文史)》每日一练试题05月06日 05-06



