2025年成考高起点《数学(理)》每日一练试题02月15日

2025年成考高起点《数学(理)》每日一练试题02月15日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、直线l1与l2：3x + 2y - 12 =0 的交点在x轴上，且l1⊥l2，则l1在y轴的截距是（）。

• A：-4
• B：
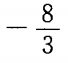
• C：4
• D：

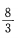
答 案：B

解 析：

2、已知正三棱柱的底面积等于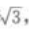侧面积等于30,则此正三棱柱的体积为（）。

• A：
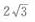
• B：
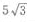
• C：
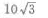
• D：

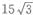
答 案：B

解 析：设正三梭柱的底面的边长为a,底面积为 设正三棱柱的高为h,侧面积为3×a×h=3×2×h=30,得h=5.则此正三棱柱的体积为底面积×高=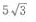

3、设F1和F2为双曲线的两焦点,点P在双曲线上,则||PF2|-|PF2||=（）。

• A：4
• B：2
• C：1
• D：

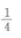
答 案：A

解 析：由题意有a²=4.a=2,由双曲线的定义,可知||PF2|-|PF2||=2a=4.(答案为A)

4、使函数y＝x²－2x－3为增函数的区间是（）。  

• A：(1，＋∞)
• B：(－∞，3)
• C：(3，＋∞)
• D：(－∞，1)

答 案：A

解 析：y’=2x-2，令y’=0得x=1,当x＞1时，y’＞0,原函数为增函数，所求区间为（1，+∞）

主观题

1、求下列函数的最大值、最小值和最小正周期： （1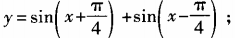）（2）y=6cosx+8sinx

答 案：  

2、计算 （1）tan5°+ cot5°- 2sec80°
（2）tan15°+cot15
（3）sin15°sin75°

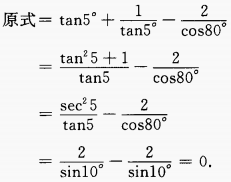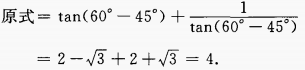答 案：（1）化切割为弦进行运算。 （2） （3）

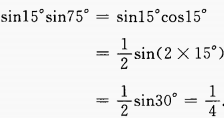
3、试证明下列各题
（1）
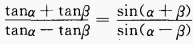
（2）

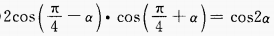
答 案：（1）化正切为正、余弦，通分即可得证。 （2）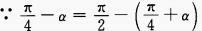

4、（1）已知tanα=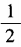，求cot2α的值； （2）已知tan2α=1，求tanα的值。

答 案：（1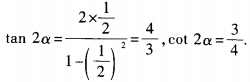）（2）由已知，得 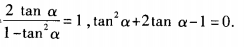解关于tanα的一元二次方程，得tanα=  

填空题

1、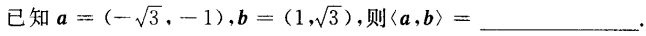  

答 案：；150°

解 析：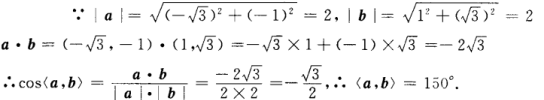

2、已知≤0＜2π，且实数x满足log₃x=2-cos²θ+sin²θ，则x的最小值是______。  

答 案：3

解 析：因为log₃x=2-（cos²θ-sin²θ）=2-cos2θ。 又log₃x中的底数3＞1，因此要使x最小，应使2-cos2θ的值最小，而其最小值为1，故x=3。