2025年成考高起点《数学(理)》每日一练试题03月29日

2025年成考高起点《数学(理)》每日一练试题03月29日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、设甲：二次不等式x²+px+q＞0的解集为空集合；乙：△=p²-4q＜0则（）。

• A：甲是乙的必要条件，但不是乙的充分条件
• B：甲是乙的充分条件，但不是乙的必要条件
• C：甲不是乙的充分条件，也不是乙的必要条件
• D：甲是乙的充分必要条件

答 案：D

解 析：由于二次不等式x²+px+q＞0的解集为空集合△=p2-4q＜0,则甲是乙的充分必要条件(答案为 D)

2、圆x²＋y²＝25上的点到直线5x＋12y－169＝0的距离的最小值是（）。

• A：9
• B：8
• C：7
• D：6

答 案：B

解 析：圆x₂+y₂=25的圆心为坐标原点(0,0),半径r=5, 圆心(0,0)到直线5x+12y-169=0的距离是 则圆x²+y²=25上的点到直线5x+12y-169=0的距离的最小值是13-5-8.(答案为B)  

3、（）。

• A：
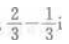
• B：
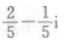
• C：
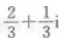
• D：

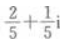
答 案：D

解 析：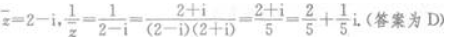

4、设f(x)=ax+b目f(0)=-2,f(3)=4,则f(2)=（）。

• A：6
• B：2
• C：1
• D：0

答 案：B

主观题

1、在正四棱柱ABCD-A'B'C'D'中， （Ⅰ）写出向量关于基底{a,b,c}的分解式 （Ⅱ）求证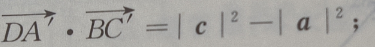： （Ⅲ）求证：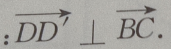  

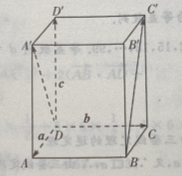
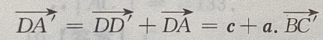
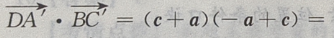
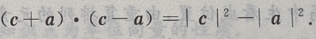答 案：(Ⅰ)由题意知(如图所示) (Ⅱ) (Ⅲ)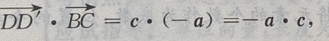 由已知，a,c是正四棱柱的棱，a,b,c两两垂直  

2、已知关于x的二次方程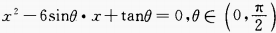的两根相等，求sinθ+cosθ的值。

答 案：

3、设函数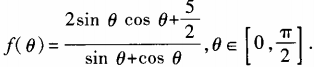（1）求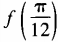；（2）求函数f（θ）最小值。

答 案：

4、求函数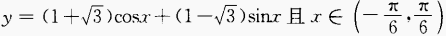上的最大值以及取得这个最大值的x。

答 案：.1 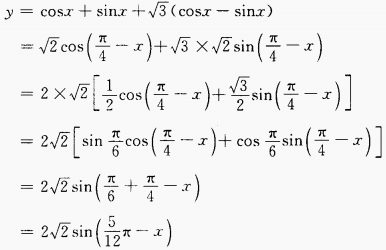函数取最大值，即y最大值=。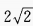

填空题

1、y=lg（sinx）的定义域是______。  

答 案：2kπ＜x＜(2k+1)π(k∈Z)

解 析：sinx＞0∴x属于第一、二象限,所以 2kπ＜x＜(2k+1)π(k∈Z)

2、ABCD是正方形，E是AB的中点，如将△DAE和△CBE分别沿虚线DE、CE折起，使AE与BE重合如图 ，设A与B重合后的点为P，则面PCD与面ECD所成的二面角为______度，PE与面ECD成______度。

答 案：二面角为30°，PE与面ECS成60角°  

解 析：（1）求面PCD与面ECD所成的二面角为多少度，就是要求出由平面PCD与平面ECD所组成的二面角的平面角，其中画出二面角的平面角是关键，因为二面角确定以后，二面角的平面角很容易画出（由二面角的平面角的定义）。求角度时，常用到勾股定理、正弦定理、余弦定理、兰垂线定理和逆定理。 （2）求PE与面ECD成多少度，就是求直线与平面所成的角是多少度。首先要找出平面的一条斜线（直线PE）和斜线的射影，斜线和射影所成的锐角，就是直线PE和平面ECD所成的角，再求出角度。 设CD的中点为F，练PF，EF
∵PC=PD，EC=ED.
∴PF⊥CD，EF⊥CD（三垂线定理）
∠PFE是二面角P-CD-E的平面角
∵PE⊥PC，PE⊥CD.
∴PE⊥平面PCD，又PF在平面PCD内
∴PE⊥PF
设正方形边长为1（如图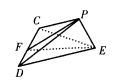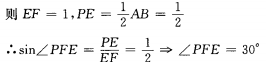） 故面PCD与面ECD所成的二面角为30°，PE与面ECS成60角°。