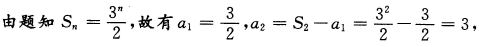2023年成考高起点《数学(理)》每日一练试题03月06日

2023年成考高起点《数学(理)》每日一练试题03月06日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、若函数f(x)是奇函数，则函数F(x)=f(x)*sin(3π/2-x)的奇偶性是（）。

• A：奇函数
• B：偶函数
• C：非奇非偶函数
• D：既是奇函数.又是偶函数

答 案：A

解 析：∵ƒ(x)是奇函数,∴ƒ(-x)=-ƒ(x)；∵F(x)=f(x)*(-cosx)=-f(x)cosx；∴F(-x)=-f(-x)cos(-x)=ƒ(x)cosx=-F(x)；∴F(x)=f(x)*sin(3π/2-x)为奇函数。

2、已知函数ƒ(x)=ax²+b的图像经过点(1，2)，且其反函数ƒ^-1(x)的图像经过点(3，0)，则函数ƒ(x)的解析式是(  )。

• A：
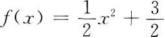
• B：ƒ(x)=-x²+3
• C：ƒ(x)=3x²+2
• D：ƒ(x)=x²+3

答 案：B

解 析：ƒ(x)过(1，2)，其反函数ƒ^-1(x)过(3，0)，则ƒ(x)又过点(0，3)，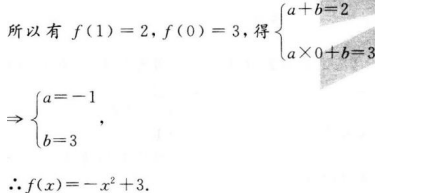  

3、(1+i)(1一i)=（）。

• A：2
• B：1
• C：0
• D：-1

答 案：A

解 析：(1+i)(1-i)=1—i2=1+1=2

4、甲、乙两人独立地破译一个密码，设两人能破译的概率分别为p1,p2，则恰有一人能破译的概率为 ( ) 

• A：1-(1-p1)(1-p2)
• B：p1p2
• C：(1-p1)p2
• D：(1-p1)p2+(1-p2)p1

答 案：D

解 析：

主观题

1、已知函数f(x)=2x³—3x²+2。(Ⅰ)求f'(x)；
(Ⅱ)求f(x)在区间[-2，2]的最大值与最小值

答 案：(I)f'(x)=6x²—6x．(Ⅱ)令f'(x)=0，解得x=0或x=1．因为f(-2)=-26，f(0)=2，f(1)=1，f(2)=6，
所以f(x)在区间[-2，2]的最大值为6，最小值为-26。

2、已知椭圆C的长轴长为4，两焦点分别为F1(-，0)，F2(，0)。 (1)求C的标准方程;(2)若P为C上一点，|PF1|-|PF2|=2，求cos∠F1PF2。

答 案：

3、已知椭圆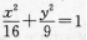，问实数m在什么范围内，过点(0，m)存在两条互相垂直的直线都与椭圆有公共点。

答 案：由椭圆方程可知，当| m|≤3时，存在过点(0，m)的两条互相垂直的直线，都与椭圆有公共点．当|m|>3时，设l1、l2是过(0，m)的两条互相垂直的直线，如果它们都与椭圆有公共点，则它们都不可能与坐标轴平行，设方程

4、正四面体ABCD内接于半径为R的球，求正四面体的棱长。  

答 案：  

填空题

1、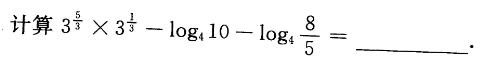

答 案：7  

解 析：该小题主要考查的知识点为对数函数与指数函数的计算.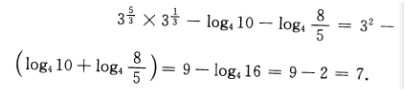

2、已知数列{an}的前n项和为，则a3=______。

答 案：9

解 析：