2025年成考高起点《数学(理)》每日一练试题03月05日
2025-03-05 12:03:24 来源：人人学历网
2025年成考高起点《数学(理)》每日一练试题03月05日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。
单选题
1、已知x+x-1=2cos40°，则x4+x-4=（）.
- A：2cos20
- B：-2cos20°
- C：2sin80°
- D：-2sin80°
答 案：B
解 析：由已知得(x+x-1)2=(2 cos 40°)2,x2+2+x-2=4cos240°,x2+x-2=2(2 cos240°-1)=2cos 80°同样可得x4+x-4=2 cos 160°=-2 cos 20°
2、
展开式中,末3项的系数(a,x 均未知) 之和为()
- A：22
- B：12
- C：10
- D：-10
答 案：C
解 析：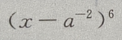
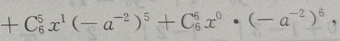末三项数之和为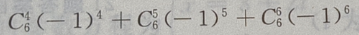
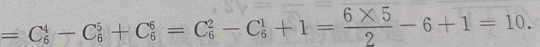
3、已知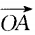
=（3，2），
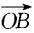=（-4，y），并其人
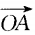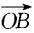⊥，则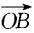的长度为（）。
- A：
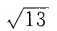
- B：
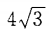
- C：
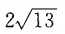
- D：
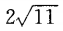
答 案：C
解 析：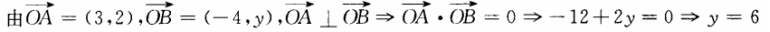
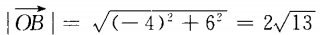
4、设log57＝m，log25＝n，则log27＝（）。
- A：
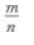
- B：
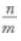
- C：m＋n
- D：m·n
答 案：D
解 析：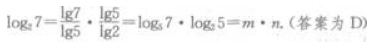
主观题
1、计算。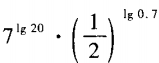
答 案：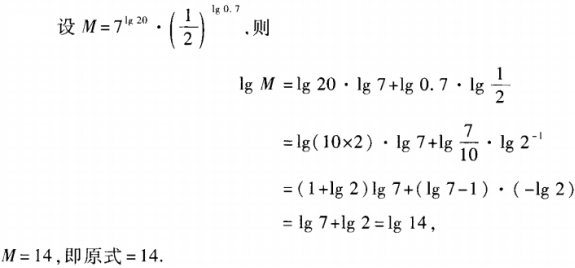
2、已知直线l的斜率为1，l过抛物线C：
的焦点，且与C交于A,B两点.(I）求l与C的准线的交点坐标；
(II）求|AB|.
答 案：(I）C的焦点为
，准线为
由题意得l的方程为
因此l与C的准线的交点坐标为
(II）由
，得
设A（x1,y1），B（x2,y2），则
因此
3、已知x+x-1=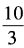
，求x2+x-2的值。
答 案：由已知，得
4、已知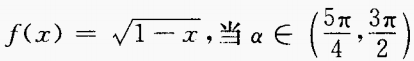
时，化简式子f(sin2α)-f(- sin2α)。
答 案：由已知得， 填空题 1、lgsinθ=a,lgcosθ=b，则sin2θ=______。
答 案：2×10a+b 解 析： 2、 答 案： 解 析：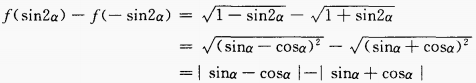
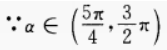∴sinα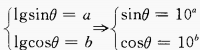
sin2θ=2sinθcosθ=2×10a×10b=2×10a+b
的展开式是（）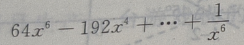
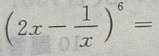
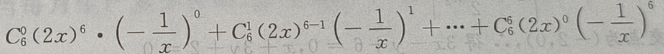
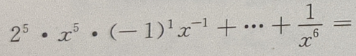
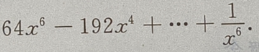
温馨提示：因考试政策、内容不断变化与调整，本站提供的以上信息仅供参考，如有异议，请考生以权威部门公布的内容为准！
- 备考交流
-
2025成考内部交流群群号：665429327
扫一扫或点击二维码入群
热门资讯
猜你喜欢
换一换
成人高考加分条件有哪些 成考怎么进行加分
01-26
2025年四川高职单招考试时间表
01-09
2025年湖南高职单招报名公告查询
01-09
山东综评报名时间2025具体时间
01-08
山东综评什么时候考试2025年 山东综评招生考试时间
01-08
山东高职单招报名时间2025年
01-07
2025年山东单招综评学校有哪些 山东综合评价招生学校名单汇总
01-07
山东省2025年上半年高等学历继续教育学士学位外语考试报名时间
01-03
