2024年高职单招《数学(中职)》每日一练试题12月19日
2024-12-19 15:48:18 来源:人人学历网
2024年高职单招《数学(中职)》每日一练试题12月19日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、函数 的定义域是()
的定义域是()
- A:

- B:

- C:
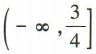
- D:
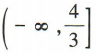
答 案:C
解 析:易知函数f(x)的表达式是二次根式,故须被开方数大于等于零.要使函数 有意义,须3-4x≥0,解得
有意义,须3-4x≥0,解得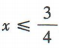 ,故函数
,故函数 的定义域为
的定义域为 .
.
2、学校运动会需要从5名男生和2名女生中选取4名志愿者,则选出的志愿者中有1名女生的不同选法的种数是()
- A:20
- B:30
- C:35
- D:40
答 案:A
解 析:选出的志愿者中有1名女生3名男生的方法种数为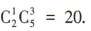
3、过点(1,2)且斜率为3的直线方程为()
- A:3x-y-1=0
- B:3x-2y+1=0
- C:x+y+1=0
- D:x+y-1=0
答 案:A
解 析:根据题意可得直线的点斜式方程为y-2=3(x-1),即3x-y-1=0.
4、已知某圆锥的侧面展开图为半圆,该圆锥的体积为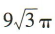 ,则该圆锥的表面积为
,则该圆锥的表面积为
- A:27π
- B:
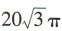
- C:

- D:16π
答 案:A
解 析:设圆锥底面的半径为r,母线长为l,由题意得2πr= πl,所以l= 2r,所以圆锥的高为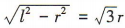 ,所以圆锥的体积为
,所以圆锥的体积为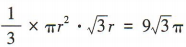 ,解得r= 3,所以圆锥的表面积为 πr2 + πrl = 9π +18π= 27π.
,解得r= 3,所以圆锥的表面积为 πr2 + πrl = 9π +18π= 27π.
填空题
1、(1-2x)3的展开式中系数最大的项是()
答 案:12x2
解 析:将(1-2x)3展开得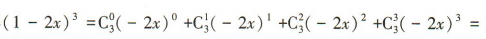
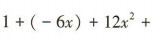
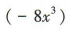 ,所以系数最大的项为12x2.
,所以系数最大的项为12x2.
2、函数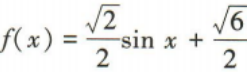 的最小值为
的最小值为
答 案: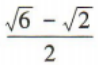
解 析: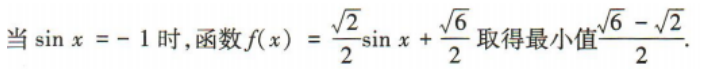
3、已知f(x)是一次函数,且其图像过点A(-2,0),B(1,5),则f(x)=()
答 案:
解 析: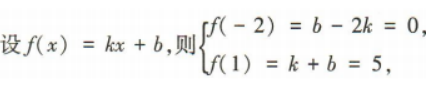

4、设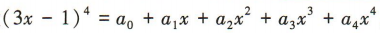 ,则
,则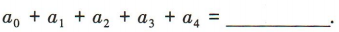
答 案:16
解 析:令x=1,得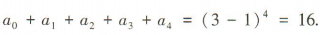
简答题
1、记等差数列{an}的前n项和为Sn,a3=5,S3=9
(1)求数列{an}的通项公式;
(2)记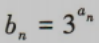 求数列{bn}的前n项和Tn.
求数列{bn}的前n项和Tn.
答 案: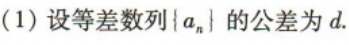
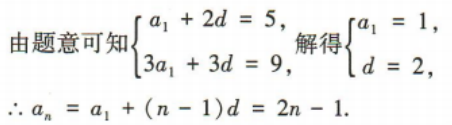

2、如图,在四棱锥P-ABCD中,底面ABCD为正方形, ,PA=PD=1.E为 AD 的中点.
,PA=PD=1.E为 AD 的中点.
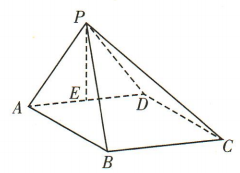 (1)证明
(1)证明 :
:
(2)求四棱锥P-ABCD 的体积.
答 案:(1)因为PA=PD=1,E为AD 的中点, 所以 又
又 所以
所以 (2)由(1)知PE为四棱锥P-ABCD 的高.
因为
(2)由(1)知PE为四棱锥P-ABCD 的高.
因为 所以
所以 所以
所以



